ラグランジュの方程式(その1)〜仮想仕事の原理と一般座標・一般力〜:1Dモデリングの勘所(39)(3/3 ページ)
一般座標
仮想仕事の原理による動的問題の解法に適した、ラグランジュの方程式の説明に入る前に、一般座標と一般力について説明する。
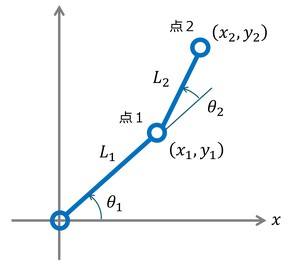
前回取り上げた回転2関節機構(図5)を例に、通常の直交座標と一般座標について述べる。
図5に示すように、直交座標では点1、点2の座標は、
である。この情報だと、合計で4つの自由度があるように見える。しかし、本問題の場合は、
という2つの制約条件があるため、自由度は2つである。このように、直交座標を本問題に適用するのは煩雑でもあり、分かりにくい。
そこで、図5に示すようにθ1,θ2なる新しい座標を用いると、点1と点2は、
で定義される。これを見れば自由度が2つであることは明白で、意味するところも直感的に理解できる。
このように、問題に応じて座標を定義したものを一般座標と呼ぶ。上記のように、直交座標は一般座標の関数として表現される。
一般力
以上のように、一般座標は便利ではあるが、座標の定義が異なってくるため、直交座標で定義された力を一般座標に変換する必要がある。
ここで、一般座標q1,q2……qnで規定されたn自由度系を考える。座標qiは互いに独立であり、今、その1つqrにδqrの仮想変位を与え、他はそのままにしたものとする。このとき、この系に作用する仮想仕事δWrは、
となる。ここで定義されるQrを、一般座標qrに関する一般力と呼ぶ。
例えば、図6に示す棒ABの両端に力が作用して、つり合っているとする。
このとき、角度qがq+δqに変化すると、
となる。従って、このときの一般座標qに関する一般力は、
となる。その際、仮想仕事δWは仮想仕事の原理により0であるため、F1a=F2bであることは明白である。
一方、n自由度の質点系においてi番目の質点に作用する力を、平面内の運動を考えてXi、Yiとすると、仮想変位中に力によってなされる仕事は、
となる。これは直交座標表現なので、一般座標表現に変換する必要がある。このとき、
であるので、これにより、
となり、
となる。このとき、Qrは一般座標qrに関する一般力となる。
図7の二重振り子を例に一般力を求めてみる。
2自由度、2質点系なので、n=2、一般座標θ1,θ2である。このとき、
となるので、これを用いて計算すると、
となる。
次回は、今回紹介した“仮想仕事の原理”の動的問題への適用、すなわちラグランジュの方程式の導出手順と適用事例について説明する。 (次回へ続く)
筆者プロフィール:
大富浩一(https://1dcae.jp/profile/)
日本機械学会 設計研究会
本研究会では、“ものづくりをもっと良いものへ”を目指して、種々の活動を行っている。1Dモデリングはその活動の一つである。
- 最新著書:1Dモデリングの方法と事例(日本機械学会)
- 研究会HP:https://1dcae.jp/
- 代表者アドレス:ohtomi@1dcae.jp
関連記事
 1Dモデリングの方法にもさまざまなアプローチがある
1Dモデリングの方法にもさまざまなアプローチがある
「1Dモデリング」に関する連載。連載第4回では、本題である1Dモデリングの方法を取り上げる。まず、1Dモデリングの方法には大きく「モデル生成」「低次元化モデリング」「類推モデリング」の3つのアプローチがあることを説明。特に本稿では1Dモデリング固有の考え方としての類推モデリングについて詳しく解説する。 0Dモデリングとは? 理論・経験に基づく理論式・経験則が究極の1Dモデリング!?
0Dモデリングとは? 理論・経験に基づく理論式・経験則が究極の1Dモデリング!?
「1Dモデリング」に関する連載。連載第3回は、理論・経験に基づく理論式・経験則が究極の1Dモデリングであることを、0Dモデリングの定義、3Dモデリングとの関係、幾つかの事例を通して説明する。また、理論・理論式を考えるに当たって重要な“単位”に関して、なぜ単位が必要なのかその経緯も含めて紹介する。 1Dモデリングとは? モデリングをさまざまな視点から捉えることで考える
1Dモデリングとは? モデリングをさまざまな視点から捉えることで考える
「1Dモデリング」に関する連載。連載第2回は、モデリングをその表現方法から2種類の“3つのモデリング”に分けて考える。次に1Dモデリングが必要となる背景について、1DCAEとMBDという2つの製品開発の考え方を紹介し、これらと1Dモデリングの関係を示す。さらに、リバース1DCAEと1DCAEを通して、より具体的に1Dモデリングのイメージを明らかにする。以上を通して、最後に“1Dモデリングとは”について考察する。 モデリングとは何か? 設計プロセスと製品設計を通して考える
モデリングとは何か? 設計プロセスと製品設計を通して考える
「1Dモデリング」に関する連載。連載第1回は、いきなり1Dモデリングの話に入るのではなく、そもそもモデリングとは何なのか? について考えることから始めたい。ものづくり(設計)のプロセス、製品そのものを構成する要因を分析することにより、モデリングとは何かを明らかにしていく。 なぜ今デライトデザインなのか? ものづくりの歴史も振り返りながら考える
なぜ今デライトデザインなのか? ものづくりの歴史も振り返りながら考える
「デライトデザイン」について解説する連載。第1回では「なぜ今デライトデザインなのか?」について、ものづくりの変遷を通して考え、これに関する問題提起と、その解決策として“価値づくり”なるものを提案する。この価値を生み出す考え方、手法こそがデライトデザインなのである。 デライトデザインとは? 3つのデザイン、類似の考え方を通して読み解く
デライトデザインとは? 3つのデザイン、類似の考え方を通して読み解く
「デライトデザイン」について解説する連載。第2回では、デライトデザインとは? について考える。まず、設計とデザインの違いについて触れ、ユーザーが製品に期待する3つの品質に基づくデザインの関係性にも言及する。さらにデライトデザインを実行する際に参考となる考え方や手法を紹介するとともに、DfXについて説明し、デライトデザインの実践に欠かせない要件を明確にする。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
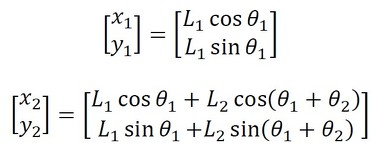 式18
式18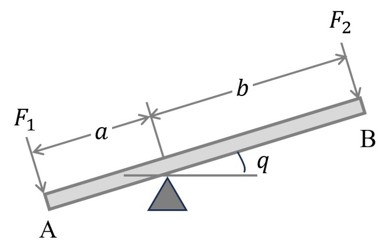
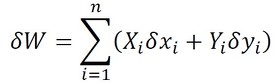 式22
式22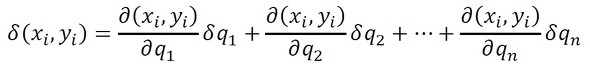 式23
式23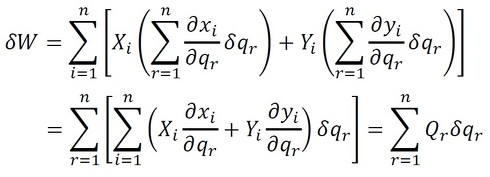 式24
式24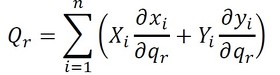 式25
式25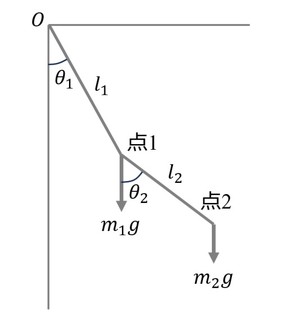
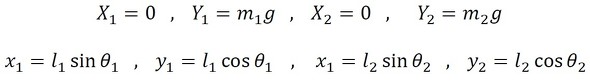 式26
式26






