ラグランジュの方程式(その1)〜仮想仕事の原理と一般座標・一般力〜:1Dモデリングの勘所(39)(2/3 ページ)
仮想仕事の原理の静的問題への適用
仮想仕事の原理による静的問題の解法
仮想仕事の原理がどのように役立つのか、動的問題について考える前に、静的問題についての適用例を図3を用いて紹介する。
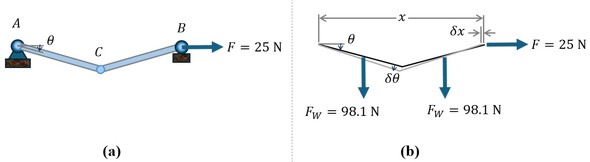
図3(a)に示すように、長さ1m、質量10kgの2本の棒が互いに回転フリーなジョイントで接合され、さらに点Aが回転フリーで固定され、自由にスライドでき、かつ回転フリーな点Bを25Nの力で引っ張って、静的につり合った状態にあるものとする。このときの角変位θがいくつになるか、仮想仕事の原理を用いて求める。
図3(b)のように、角変位θのときの点Bのx方向座標および各棒の重心位置のy方向座標の仮想変位は式6となる。
一方、この仮想変位による仮想仕事について、仮想仕事の原理から0とすると、
となる。この式に必要な値を代入すると、
となり、これを整理すると、
となり、最終的には、
が求まる。
通常の方法による静的問題の解法
次に、通常の方法で図3(a)の問題を解いてみよう。このとき、さまざまな方法が考えられるが、その一例を図4を用いて説明する。
まず、図4(a)に示すように、各点に作用する力を定義すると、x方向、y方向の力のつり合い式と、点A周りのモーメントのつり合い式は以下となる。
式11を未知数Ax、Ay、Byについて解くと(第3式のcosθは両辺から消去できるので計算には影響しない)、
となる。
次に、右側の棒だけに着目すると図4(b)となる。図4(a)と同様に力とモーメントのつり合い式を考えると、
となる。これを解くと、
となり、最終的には、
となる。
力学を理解する上では(教育的には)通常の方法がよいと個人的には考えるが、実用的には(特に構造が複雑な場合には)、仮想仕事の原理を用いる方が間違いが少ない。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
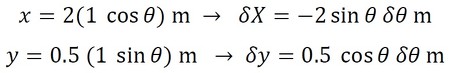 式6
式6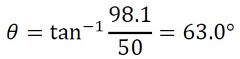 式10
式10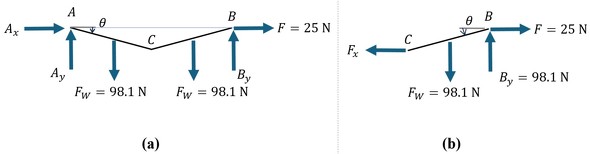
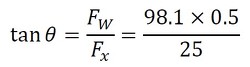 式14
式14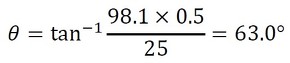 式15
式15





