溶接部の疲労強度(その2):CAEを正しく使い疲労強度計算と有機的につなげる(11)(1/6 ページ)
金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第11回は、前回に引き続き「溶接部の疲労強度」について取り上げる。
溶接部の疲労強度計算は、ここで述べる応力レンジの計算方法で完結です。そして、異なるアプローチで溶接部の強度評価方法を簡単に説明します。読者の方々が習ったはずだが一度も使ったことのない破壊力学です。
応力レンジの計算
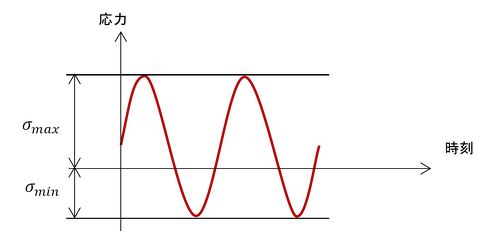
図1に応力の時間変化を示します。応力レンジは式1で定義されます。連載第10回と異なる点は最小応力σminがマイナス値であることです。プラス値の応力は引張応力、マイナス値の応力は圧縮応力であることはお約束です。
最小応力σminがマイナス値のときの応力レンジは式2となります。
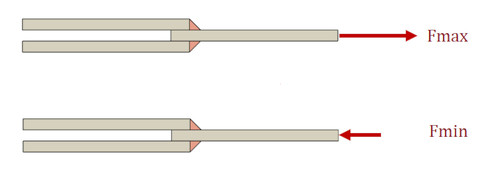
図1の荷重を図示すると、図2のようになります。
荷重を代入すると式3となります。ただし、Fminはマイナス値です。
数値を代入しましょう。以下となります(式4)。
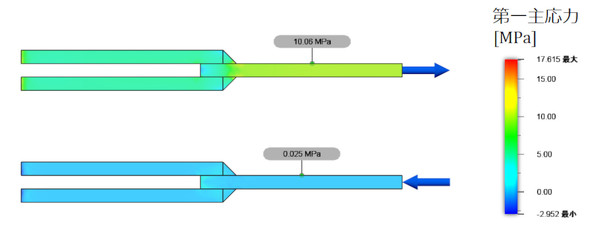
連載第10回で応力レンジは主応力で計算すると述べました。図3に第一主応力分布を示します。
圧縮応力側の第一主応力がほぼゼロとなって、式2に数値を代入しても応力レンジがうまく求まらなくなりました。圧縮応力側を第三主応力とすれば応力レンジの計算結果は式4と一致しますが、これは荷重の方向が正反対のときで、かつ運良く圧縮応力と気付いた場合に限ります。
主応力同士の引き算はできない
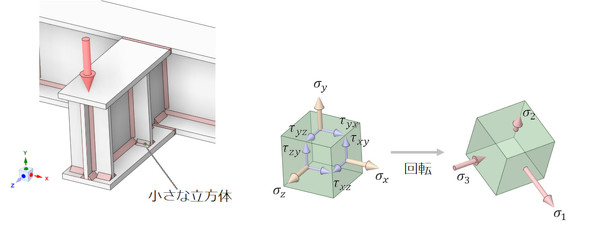
主応力同士の引き算はやってはいけません。その理由を説明するために3次元版の主応力を説明します。図4に溶接構造物内の小さな立方体に作用する応力成分を示します。応力成分は6成分あります。
この小さな立方体を回転させると各面に作用する応力は変化しますが、うまく回転させると、せん断応力成分がゼロになるような回転位置があります。このときの面に垂直な応力成分を「主応力」といいます。主応力は次式で計算できます。主応力は3次方程式の3根です。
求まった3根のうち、大きいものから第一主応力σ1、第二主応力σ2、第三主応力σ3とします。ソフトによっては最大主応力、中間主応力、最小主応力と表示されますが、最大主応力の呼称を用いると、第一主応力の最大値のことを「最大主応力の最大値」と表現できてしまい訳が分からなくなるので、ここでは第一主応力と呼んでいます。
大きいものが第一主応力なので、第一主応力は引張応力になることがほとんどです。第三主応力は圧縮応力になります。主応力の方向は応力状態により異なります。荷重の符号が正反対のときのみ第一主応力と第三主応力の差が応力レンジに一致しますが、これは特別な場合です。
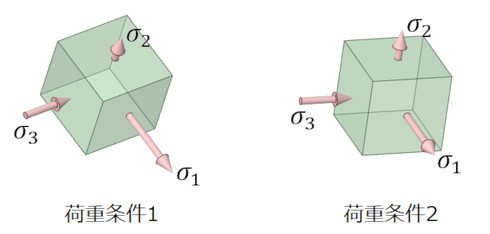
図5に、2つの荷重条件における主応力を示します。第一主応力σ1の方向が違うため、その引き算は無効ですね。
おまけに言いますと、ミゼス相当応力も引き算はできません。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- キヤノン社員が技能五輪国際大会の工業デザイン技術職種で日本代表に
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本

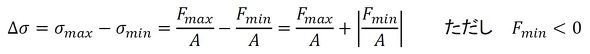 式3
式3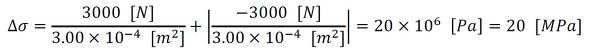 式4
式4