溶接部の疲労強度(その2):CAEを正しく使い疲労強度計算と有機的につなげる(11)(2/6 ページ)
荷重方向が変化するときの応力レンジの計算方法
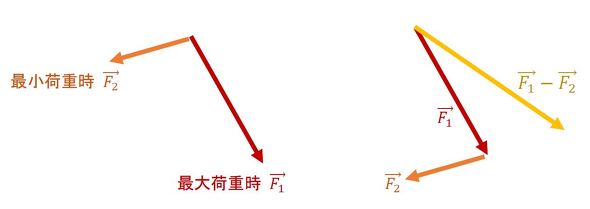
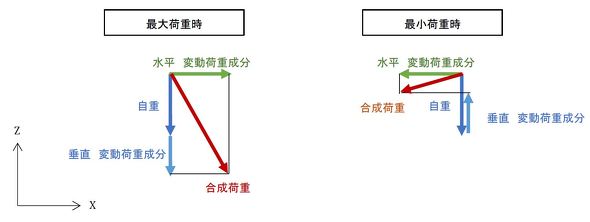
最大荷重時と最小荷重時の荷重の方向が正反対にならない例として、図6に示すようなZ方向荷重が重力プラス変動荷重の場合があります。Z方向荷重について述べると、最大荷重は自重と変動荷重成分の和、最小荷重は自重と垂直荷重成分の差となります。そして、X方向荷重について述べると、最大荷重はプラスの変動荷重成分、最小荷重はマイナスの変動荷重成分です。この結果、最大荷重時と最小荷重時で合成荷重(赤色ベクトル)は図示したように反転しません。そして、前述したように最大荷重時の主応力と最小荷重時の主応力の引き算はできません。
このような場合、応力レンジはどのようにして求めればよいでしょうか。文献は見当たらないので自分で考えることにしました。提案として、以下のものが考えられます。
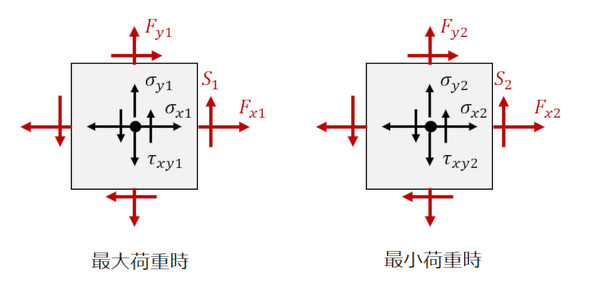
- (1)図4に示した座標軸に垂直方向の6つの応力成分σx、σy、σz、τxy、τyz、τzxは引き算ができる。つまり、最大荷重による6つの応力成分σx1、σy1、σz1、τxy1、τyz1、τzx1と最小荷重による6つの応力成分σx2、σy2、σz2、τxy2、τyz2、τzx2との差は有効である
- (2)これらの差に基づく6つの応力成分(σx1−σx2、σy1−σy2、σz1−σz2、τxy1−τxy2、τyz1−τyz2、τzx1−τzx2)から求めた第一主応力を応力レンジとして使えないだろうか
- (3)主応力は次式で求める
上記の提案が有効かを調べましょう。少し骨が折れますが、図7に示すような最大荷重と最小荷重の方向が異なる例を計算してみましょう。
最大荷重時の解析結果を図8に示します。
図9に示す応力評価点の応力値をテキストファイル形式で出力して「Excel」に取り込みました。これを表1に示します。これから3次方程式を解くマクロプログラムを作成し、主応力を求めました。その結果を表2に示します。
応力レンジは31.39[MPa]となりました。
少し乱暴な応力レンジの計算をしてみましょう。「主応力の引き算はダメ」と説明しましたが、最大荷重時のσ1と最小荷重時のσ3の差を計算してみます。その結果、32.25[MPa]となり、前述した31.39[MPa]に近い値となりました。甚だ乱暴な発想ですが、表2のσ1は良い線いっているように思えます。
以上の作業はかなり面倒なものでした。そして、この方法では着眼した1節点の応力レンジしか求まりませんので、応力レンジの分布、つまりコンター図が描けません。いい方法はないでしょうか。筆者が会社勤めをしていた当時、「荷重ベクトルの差を荷重として解析すると、その結果が応力レンジなるのでは?」との提案を受けたことがあります。図10の黄色のベクトルが荷重ベクトルの差です。図に示すように、荷重ベクトル差である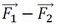 ベクトル(黄色)は、
ベクトル(黄色)は、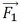 (赤色)や
(赤色)や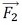 (橙色)とはあさっての方向を向いているので、あさっての方向を向く荷重ベクトルに何の意味があるのかと思い、この提案を却下したことがあります。
(橙色)とはあさっての方向を向いているので、あさっての方向を向く荷重ベクトルに何の意味があるのかと思い、この提案を却下したことがあります。
しかし、このとき一応は計算しておこうかと思い、2次元平面応力状態で下記の計算をしました。図11に、最大荷重時と最小荷重時の荷重と応力を示します。最大荷重と最小荷重が交互に作用したときの応力レンジを求めましょう。Fx1、Fy1、Fx2、Fy2は垂直荷重、S1、S2はせん断荷重です。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

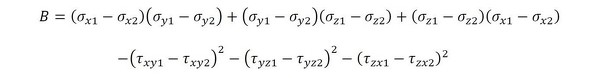 式11
式11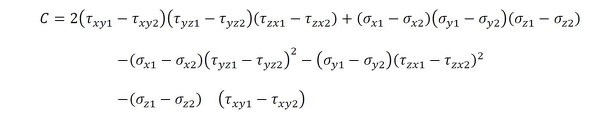 式12
式12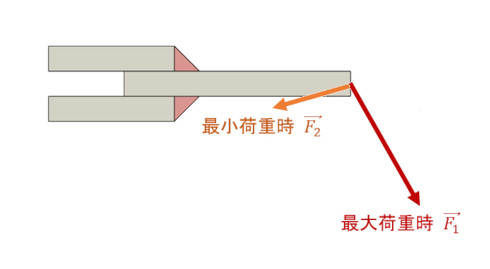
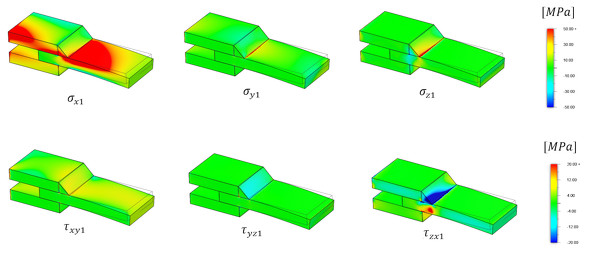
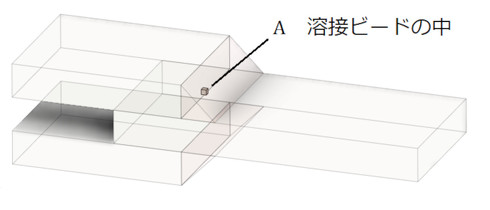

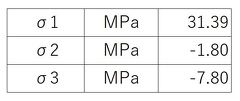 表2 応力差から求めた主応力
表2 応力差から求めた主応力