溶接部の疲労強度(その2):CAEを正しく使い疲労強度計算と有機的につなげる(11)(4/6 ページ)
破壊力学:応力拡大係数
紙面が余りましたので、破壊力学を使ってすみ肉溶接の強度評価をしてみましょう。あらすじは以下です。
- すみ肉溶接部をき裂として捉える
- すみ肉溶接部の応力拡大係数範囲ΔKを求める
- ΔKが下限界応力拡大係数範囲ΔKthよりも小さければき裂は進展しないため、溶接部は疲労破断しないと判断する
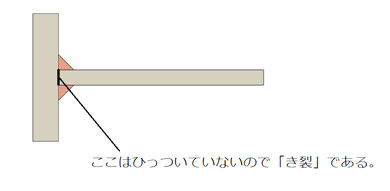
図13に、すみ肉溶接を示します。ひっついていない部分があるので、これを「き裂」として捉えることができます。角Rがゼロの応力集中係数は無限大だったので、き裂先端の応力は無限大となります。
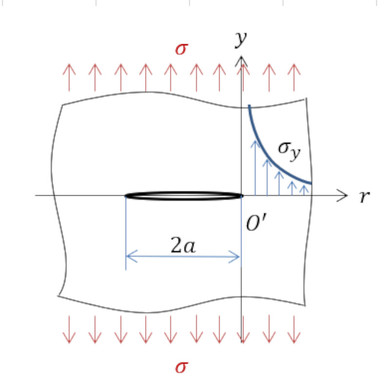
応力拡大係数Kを簡単に説明します。応力集中係数αと混同しないことに注意が必要です。無限に大きな2次元的な板に長さ2aのき裂がある状態を図14に示します。板の上下方向の遠い所に均一な応力σが作用しているとします。Y方向応力は式31で表されます(参考文献[1]〜[4])。
上式を級数展開すると式32になります。
r≪aでは、上式の第1項が他の項と比べて圧倒的に大きくなるため、第2項以降を無視することにすると、σyは式33となります。
上式を変形します。
今、K=σ√πaとしました。このKが応力拡大係数で、単位はMPa√mです。き裂には図15に示す3つのモードがあります。
最初はモードIIであっても、き裂はモードIになるように進行方向を変えるとのことなので、モードIについて述べます。図16に、き裂近傍の応力を示します。応力は次式で求められます。
き裂にはいろいろな形状のものがあるのですが、その応力分布は式35〜37と同じ形です。異なるのは応力拡大係数だけです。これを「破壊力学における相似則」といいます。いろいろな形状の応力拡大係数は式39で表され、係数Fは形状により決まります。係数Fは参考文献[1]〜[4]から見つけられます。
応力拡大係数は、「き裂先端の応力は無限大であるが、荷重が大きいとそれに比例して大きくなるので、無限大の前に付ける比例定数のようなもの」と解釈しております。
参考文献:
- [1]日本機械学会|よく分かる破壊力学・弾性力学|講習会資料(2013)
- [2]日本機械学会|機械工学便覧 基礎編 A4 材料力学|丸善(1992)
- [3]日本機械学会|材料力学ハンドブック<応用編>|(2008)
- [4]宮本|破壊の力学|コロナ社(S47)
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

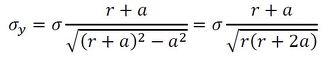 式31
式31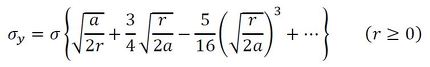 式32
式32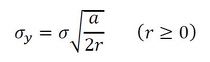 式33
式33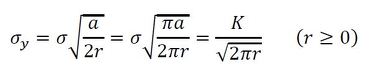 式34
式34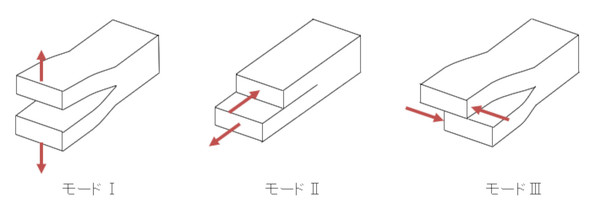
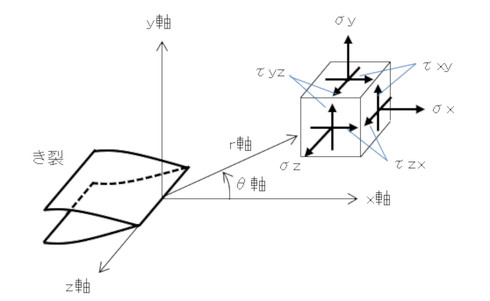
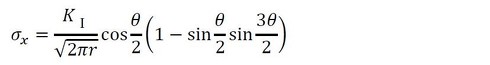 式35
式35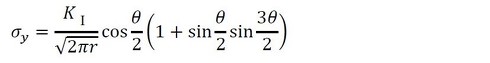 式36
式36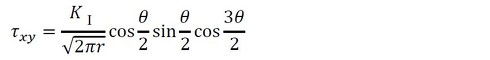 式37
式37





