溶接部の疲労強度(その2):CAEを正しく使い疲労強度計算と有機的につなげる(11)(3/6 ページ)
まず、式9〜12の方法です。zに関する応力は全てゼロなのでA、B、Cは以下となります。
そして、以下に記した応力を代入します。
式9は以下となります。
式18より、1つの根はゼロです。残り2つの根は以下となります。
第一主応力がプラス値、第三主応力がマイナス値とすると、主応力は以下となります。
では、図10に示したように荷重ベクトルの引き算をします。荷重は以下となります。
応力は以下となります。
ベクトルの引き算をした場合もzに関する応力は全てゼロなのでA、B、Cは以下となります。
応力を代入します。
式19にA、Bを代入します。
式がたくさん出てきましたが、式20と式28は一致しました。つまり、荷重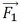 による6つの応力成分σx1、σy1、σz1、τxy1、τyz1、τzx1と荷重
による6つの応力成分σx1、σy1、σz1、τxy1、τyz1、τzx1と荷重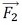 による6つの応力成分σx2、σy2、σz2、τxy2、τyz2、τzx2との差から求めた主応力と、2つの荷重の差
による6つの応力成分σx2、σy2、σz2、τxy2、τyz2、τzx2との差から求めた主応力と、2つの荷重の差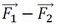 から求めた主応力は一致しました。ということは、荷重の差
から求めた主応力は一致しました。ということは、荷重の差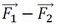 を荷重条件としてCAE解析を1回行うと、その結果の第一主応力分布が応力レンジ分布となります。これならば3次方程式を解くこともなく、解析も1回で済みますね。
を荷重条件としてCAE解析を1回行うと、その結果の第一主応力分布が応力レンジ分布となります。これならば3次方程式を解くこともなく、解析も1回で済みますね。
2つの荷重の差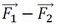 はベクトルであって、ベクトル
はベクトルであって、ベクトル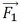 、
、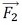 とは全然異なるあさっての方向を向いていたため、前述したことは直観的には気付かないのですが便利な方法だと思います。
とは全然異なるあさっての方向を向いていたため、前述したことは直観的には気付かないのですが便利な方法だと思います。
では、数値を代入しましょう。図12に最大荷重と最小荷重の差(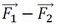 )を荷重とした解析結果を示します。ここから、図9の応力評価点の主応力を読み取った結果を表3に示します。今回使ったソフトではσ2を出力できなかったのですが、σ1とσ3は表2の値と一致しました。
)を荷重とした解析結果を示します。ここから、図9の応力評価点の主応力を読み取った結果を表3に示します。今回使ったソフトではσ2を出力できなかったのですが、σ1とσ3は表2の値と一致しました。
ここで提案です。
最大荷重時の荷重ベクトルと最小荷重時の荷重ベクトルが正反対でない場合、最大荷重時の荷重ベクトルと最小荷重時の荷重ベクトルの差のベクトルを荷重ベクトルとして解析し、その第一主応力を応力レンジとする。
最大荷重時の荷重方向と最小荷重時の荷重方向が正反対にならないときの応力レンジの求め方は、どの文献にも見当たらないので、読者の皆さんは、
- ここでの方法を採用する
- 自分で考える
- 次に述べる破壊力学を使う
の三者一択になるのでしょうか。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現

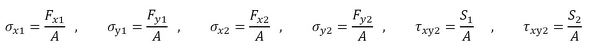
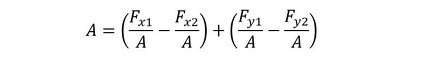 式15
式15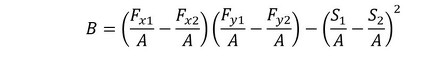 式16
式16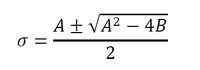 式19
式19
 式22
式22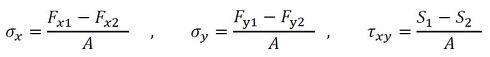 式24
式24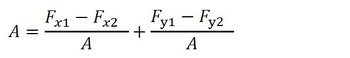 式26
式26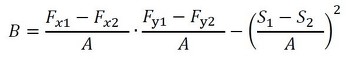 式27
式27
 式30
式30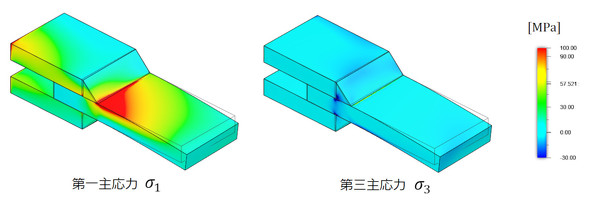
 表3 最大荷重と最小荷重の差(
表3 最大荷重と最小荷重の差(





