N0＝120000［rpm］＝2000［rps］＝2000×2π［rad/s］
a＝1.2［m³/min］＝1／50［m³/s］
b＝20000［Pa］
α＝10⁸［Pa・s/m⁶］
E＝22［V］
R＝1［Ω］
RB＝0.21［Ω］
KT＝8.8×10^-4［Nm/A］
KE＝8.8×10^-4［Vs/rad］
BC＝3［Ah］

　以上の値と、図7の5つの式をModelicaスクリプトで表現、解析を実施する。

model CordlessCleaner
 import Modelica.Constants.pi;
 Real P (start=10000);
 Real Q (start=0.01);
 Real T;
 Real N (start=12000);
 Real Nrpm;
 Real Qmin;
 Real W;
 Real I;
 parameter Real a=1/50;
 parameter Real b=20000;
 parameter Real N0=2000*2*pi;
 parameter Real alfa=1e8;
 parameter Real E=22;
 parameter Real R=1;
 parameter Real Rb=0.21;
 parameter Real Kt=8.8e-4;
 parameter Real Ke=8.8e-4;
equation
 P=-(b/a)*Q*(N/N0)+b*(N/N0)^2;
 P=alfa*Q*abs(Q);
 P*Q=T*N;
 N=(E/Ke)-(R+Rb)*T/Ke/Kt;
 Nrpm=N*60/2/pi;
 Qmin=Q*60;
 W=P*Q;
 I=(E-Ke*N)/(R+Rb);
end CordlessCleaner;

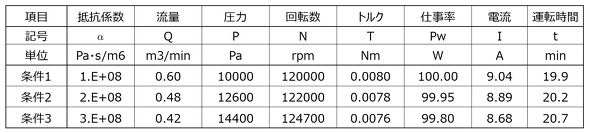
　表1に解析結果を示す。条件1は開放時（ブラシが床から離れている）、条件2は使用時でブラシを軽く床に当てている状態、条件3は同じく使用時でブラシを強く床に当てている状態を想定している。条件（抵抗）により、流量、圧力、回転数などが変化していることが分かる。

表1　解析例［クリックで拡大］

　ここでは、条件1の場合にファンが最高のパワーを発揮するようにシステム抵抗を設定している。すなわち、表1の条件1の仕事率（パワー）100Wはこのファンの最大パワーである。また、モーター性能も条件1のときに最高のパワーを発揮するように設定している。

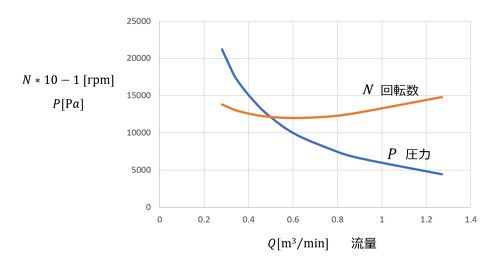
　一方、条件2、条件3は、条件1よりシステム抵抗が大きいため、図5のファン特性から類推できるように、流量は減少するが圧力は上昇し、結果としてパワーは条件1より小さくなるが、その減少度合いは無視できるレベルである。また、パワー（負荷）が減少することにより、条件2、条件3の回転数は条件1より大きくなっている。この3条件では仕事率に差がないため、運転時間（パワーに反比例）も3つの条件でほとんど変わらない約20分となっている。

　図5では、ファン特性を一次式（直線）で近似したが、コードレスクリーナーを制御なしで運転するとファンの特性は図8のように変化する。すなわち、実際の製品を使った測定では種々の要因が絡み合った形式（この場合は条件により回転数が変化）でデータを取得していることになる。これは、ファン特性を実験的に求める場合には、回転数を一定にした条件で圧力と流量を測定する必要があることを意味する。

図8　制御なしで運転した時のファン特性［クリックで拡大］

Modelicaによるモデリング

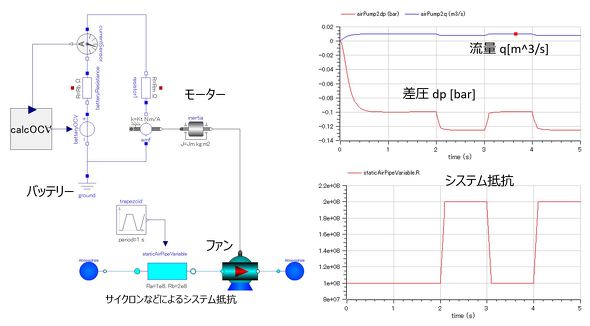
　前回のミニ四駆の場合と同様に、Modelicaを用いてモデリングした例を図9に示す（参考文献［1］）。

図9　Modelicaによるコードレスクリーナーのモデリング［クリックで拡大］

　この結果より、起動して0.8秒後に流量および圧力が安定していることが分かる。さらに図では、起動2秒後から、ブラシの接地／開放を1秒ごとに繰り返している状況を示している。ブラシを接地すると、システム抵抗が増え（図9の右下図）、これに伴い、差圧がマイナス側に大きくなり、流量がわずかに減っている（図9の右上図）ことが分かる。

参考文献：

［1］大富、平野｜製品・システムの複合化に対応した設計を支援～対話形式で解きほぐすModelica活用法～｜第25回コードレスクリーナをモデリングする｜機械設計2022年1月特別増大号

　次回は、スピーカーのモデリングについて考える。　（次回へ続く）

⇒連載バックナンバーはこちら

筆者プロフィール：

大富浩一（https://1dcae.jp/profile/）

日本機械学会設計研究会
本研究会では、“ものづくりをもっと良いものへ”を目指して、種々の活動を行っている。1Dモデリングはその活動の一つである。

研究会HP：https://1dcae.jp/
代表者アドレス：ohtomi@1dcae.jp

1Dモデリングの方法にもさまざまなアプローチがある
「1Dモデリング」に関する連載。連載第4回では、本題である1Dモデリングの方法を取り上げる。まず、1Dモデリングの方法には大きく「モデル生成」「低次元化モデリング」「類推モデリング」の3つのアプローチがあることを説明。特に本稿では1Dモデリング固有の考え方としての類推モデリングについて詳しく解説する。
0Dモデリングとは？　理論・経験に基づく理論式・経験則が究極の1Dモデリング!?
「1Dモデリング」に関する連載。連載第3回は、理論・経験に基づく理論式・経験則が究極の1Dモデリングであることを、0Dモデリングの定義、3Dモデリングとの関係、幾つかの事例を通して説明する。また、理論・理論式を考えるに当たって重要な“単位”に関して、なぜ単位が必要なのかその経緯も含めて紹介する。
1Dモデリングとは？　モデリングをさまざまな視点から捉えることで考える
「1Dモデリング」に関する連載。連載第2回は、モデリングをその表現方法から2種類の“3つのモデリング”に分けて考える。次に1Dモデリングが必要となる背景について、1DCAEとMBDという2つの製品開発の考え方を紹介し、これらと1Dモデリングの関係を示す。さらに、リバース1DCAEと1DCAEを通して、より具体的に1Dモデリングのイメージを明らかにする。以上を通して、最後に“1Dモデリングとは”について考察する。
モデリングとは何か？　設計プロセスと製品設計を通して考える
「1Dモデリング」に関する連載。連載第1回は、いきなり1Dモデリングの話に入るのではなく、そもそもモデリングとは何なのか？　について考えることから始めたい。ものづくり（設計）のプロセス、製品そのものを構成する要因を分析することにより、モデリングとは何かを明らかにしていく。
なぜ今デライトデザインなのか？　ものづくりの歴史も振り返りながら考える
「デライトデザイン」について解説する連載。第1回では「なぜ今デライトデザインなのか？」について、ものづくりの変遷を通して考え、これに関する問題提起と、その解決策として“価値づくり”なるものを提案する。この価値を生み出す考え方、手法こそがデライトデザインなのである。
デライトデザインとは？　3つのデザイン、類似の考え方を通して読み解く
「デライトデザイン」について解説する連載。第2回では、デライトデザインとは？　について考える。まず、設計とデザインの違いについて触れ、ユーザーが製品に期待する3つの品質に基づくデザインの関係性にも言及する。さらにデライトデザインを実行する際に参考となる考え方や手法を紹介するとともに、DfXについて説明し、デライトデザインの実践に欠かせない要件を明確にする。