EVのモデリングを「ミニ四駆」で考える〜バッテリー、モーター、走行の連成問題、現象を本質的に捉えてシンプルに表現〜:1Dモデリングの勘所(10)(1/4 ページ)
「1Dモデリング」に関する連載。前回行った「ミニ四駆」の構成要素の原理理解、定式化を受けて、今回はミニ四駆全体系のモデリングを行い、解析を実行する。さらに現象を理解する方法としてモデリング結果を図で表現することの有用性に触れる。最後に、「Modelica」によるミニ四駆のモデリング例を示す。
前回は、タミヤの「ミニ四駆」の構成要素であるバッテリー、モーター、ギア、走行系に関して、その原理を理解し、定式化を行った。
今回はこの結果を受けて、ミニ四駆全体系のモデリングを行う。モデリング結果を基に、実際に解析を行うには、各種パラメータを決定する必要がある。その各パラメータの決定方法について述べ、解析を実行し、考察を行う。次に、現象を理解する方法としてモデリング結果を図(グラフ)で表現することの有用性に触れる。最後に、モデリング言語「Modelica」によるミニ四駆のモデリング例を示す。
※注:「ミニ四駆」は株式会社タミヤの登録商標です。
「ミニ四駆」のモデリング
ミニ四駆全体系のモデリングを行うに際して重要なことは、このモデリングを通して何を知りたいのかを明確にしておくことである。多くの場合、知りたいことは「ミニ四駆がどのくらいの速度で走るのか/どのくらいの距離を走るのか」ではないだろうか。そこで、これを目的に全体系のモデリングを考える。なお、ここでは説明を分かりやすくするため定常状態を考えることにし、バッテリーのSOC(充電率)も考慮しないことにする。
前回の知見を基に考えると、速度vはモーター回転数をωM、ギア比をGr、タイヤの半径をrとすると、
となる。なお、色の付いた字は未知数(計算によって求まる値)である。また、走行距離を知るには、速度と走行時間が必要で、走行時間はバッテリーの電流から求まる。電流Iは、トルクTMを、トルク定数KTとすると、
となる。さらに、モーターの特性式からモーター回転数とモータートルクの関係が、
で表現できる。ここに、Eはバッテリーの電圧、RBはバッテリーの内部抵抗、RMはモーターの巻き線抵抗、KEは起電力定数である。モータートルクTMはギアを介して、けん引力Ftに変換される。けん引力はギア損失をηgとすると、
と表現できる。最後にけん引力と走行抵抗(転がり抵抗、空気抵抗)は釣り合っているので、
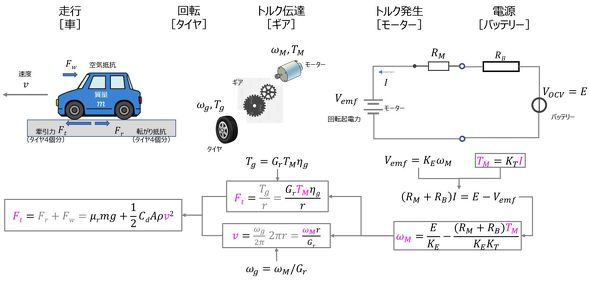
となる。以上の5つの式に対して、5つの未知数(v、ωM、TM、I、Ft)が存在するので解くことができるはずである。以上の流れを図1に示す。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現
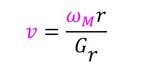 式1
式1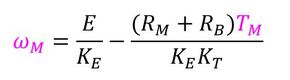 式3
式3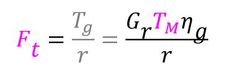 式4
式4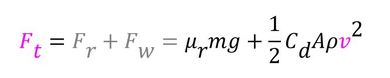 式5
式5