EVのモデリングを「ミニ四駆」で考える〜バッテリー、モーター、走行の連成問題、現象を本質的に捉えてシンプルに表現〜:1Dモデリングの勘所(10)(3/4 ページ)
解析結果と考察
図1の5つの式を基に未知数、パラメータ、方程式をModelicaで直に書くと以下となる。ここに、g_nは重力加速度を意味する。
model mini4Drive import Modelica.Constants.g_n; Real Tm; Real I; Real Om; Real Ft; Real v; parameter Real Rm=1; parameter Real Rb=0.8; parameter Real E=3; parameter Real Ke=1.2e-3; parameter Real Kt=1.2e-3; parameter Real Gr=5; parameter Real Ita=0.6561; parameter Real r=0.015; parameter Real Mu=0.1; parameter Real m=0.1; parameter Real Cd=0.3; parameter Real A=0.004; parameter Real Ro=1.205; equation Tm=Kt*I; Om=(E/Ke)-(Rm+Rb)*Tm/(Ke*Kt); Ft=Gr*Tm*Ita/r; v=Om*r/Gr; Ft=Mu*m*g_n+(1/2)*Cd*A*Ro*v^2; end mini4Drive;
上式を解くと、
- けん引力:Ft=0.120[N]
- 電流:I=0.456[A]
- モーター回転数:ωM=1817[rad/s]=17349[rpm]
- モータートルク:TM=0.000547[Nm]
- 速度:v=5.45[m/s]=19.6[km/h]
という結果が得られる。ここで、バッテリーの容量を1Whとすると、走行時間は、
となり、走行距離は、
となる。
現象の理解
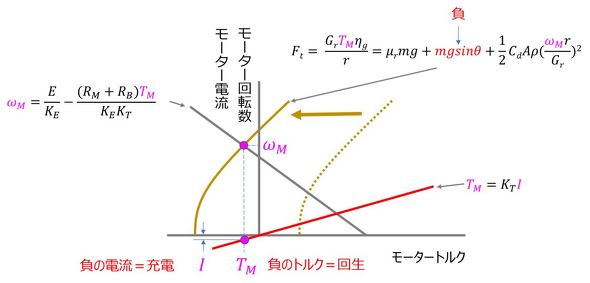
以上、現象の理解を方程式で表現することで行った。これはこれで重要なことであるが、できれば図として現象を直感的に理解できると役に立つ。ミニ四駆の主要要素はバッテリー、モーター、走行系であり、この3つの要素を支配する現象を1つの図に表現することを試みる。モーターは既に述べたように、回転数ωMとトルクTMの関係式で表現できる。バッテリー電流はトルク定数を介して、モータートルクにひも付けられる。一方、走行系は、
で表現でき、この式に図4のFtとvの定義式を代入すると次式が得られる。
以上のバッテリー、モーター、走行系に関する式を1つの図で表現すると図5となる。すなわち、モーターの式と走行系の式の交点がモーターの運転点(TM、ωM)で、このトルクTMと電流の式の交点が電流値Iとなる。
図5の図表現による現象の理解の応用例として、急勾配の下り坂を走行している状況を考える。この場合、走行系の式は、
となる。mgsinθは急勾配の下り坂を下る際の力で負の値となる。従って、急勾配の下り坂を下る際の走行系の式(二次曲線)は、図6に示すように左側に平行移動する。そうすると、負のトルク、負の電流が発生する。すなわち、バッテリーが充電状態となる。これを「回生」という。図6では分かりやすくするために、モーター特性は変わらないとしているが、実際には、回生制動(回生ブレーキ)により、走行中にモーターに制動トルクを発生させることで、図6に示すよりも大きな電気エネルギーを回収できる。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
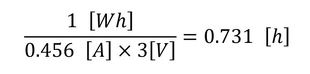 式12
式12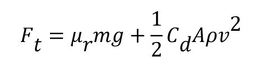 式14
式14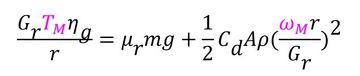 式15
式15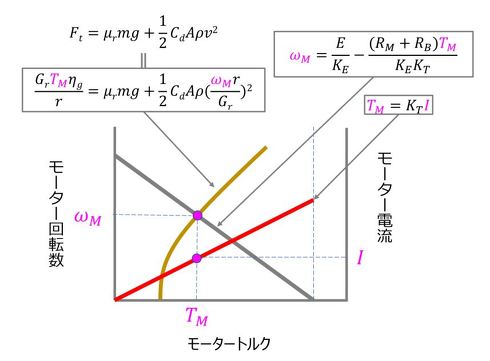
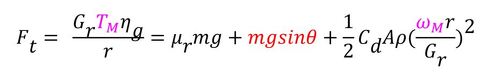 式16
式16