非線形解析のフローと幾何学的非線形性:いまさら聞けない 非線形構造解析入門(3)(4/5 ページ)
» 2022年08月01日 07時00分 公開
[水野操 mfabrica合同会社 社長/3D-GAN,MONOist]
トータルラグランジュ法とアップデートラグランジュ法、
応力測度とひずみ測度
非線形の問題を解く際、どのひずみを使用するかでその手法が変わってきます。「Cauchy応力(真応力)」で記述されたCauchyの第1運動法則を解くものが「アップデートラグランジュ法」、2ndピオラキルヒホッフ応力で記述されたCauchyの第1運動法則を解くものが「トータルラグランジュ法」になります。どの手法で非線形の問題を解くかで、使用する応力とひずみの測度が決まっています。
トータルラグランジュ法では、ひずみはグリーンラグランジュひずみ、応力は2ndピオラキルヒホッフ応力が用いられ、アップデートラグランジュ法の定式化の場合には、ひずみは対数ひずみ(真ひずみ)、応力はCauchy応力(真応力)が使用されます。
解析ソフトを使用する観点から重要なのは、自分がどのような応力、あるいはひずみを使用しているのかです。ということで、非線形解析をやる上で必要な応力とひずみについて説明したいと思います。
応力について
- Cauchy応力(真応力):
この応力は、現在の断面積と現在の変形状態を基準として評価される応力になります。変形状態を評価する際に、当然基準となる状態が必要になるわけですが、現在の増分の直前に終了した増分の状態を基準として現在の状態を評価することになります。この応力をCauchy応力、あるいは真応力と呼びます。単純な1軸の問題であれば、載荷している荷重を現在の断面積で割って得られた応力ということになります。これは前述の通り、アップデートラグランジュ法で使用される応力になります。
- 2ndピオラキルヒホッフ応力:
正直なところ、前述のCauchy応力は比較的イメージしやすい応力だと思うのですが、この2ndピオラキルヒホッフ応力は以下の式4を見ても直感的に理解するのが難しいです。実際、理論の展開において必要な応力なのですが、物理的な意味は希薄です。こちらはトータルラグランジュ法で使用される応力になります。
参考までに、一般的に使用される材料力学の応力は「公称応力」というものになります。これは、微小変形、微小ひずみの問題、つまり線形問題で使用する応力で、1軸の問題であれば、荷重を最初の断面積で割ったものになります。定義は式5で表せます。
ひずみについて
- 対数ひずみ(真ひずみ):
このひずみは、現在の長さを評価の基準として用いるひずみになり、前述のCauchy応力とともに、アップデートラグランジュ法を用いる際に使用されるひずみになります。このひずみの定義は以下の通りとなります。
- グリーンラグランジュひずみ:
こちらのひずみは初期の長さを基準とした上で、回転を考慮したひずみということになります。1軸問題の場合には式7のようになりますが、応力同様に直感的には分かりにくいものになっています。
参考までに「公称ひずみ(工学ひずみ)」も示しておきます。こちらも公称応力と同様に、材料力学の本などに示されている私たちに一番なじみのあるひずみの測度になります。1軸問題では以下のようになります。
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentsPR
Pickup ContentsPR
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
Special SitePR
あなたにおすすめの記事PR

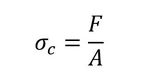 式3
式3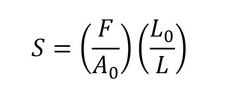 式4
式4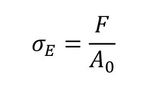 式5
式5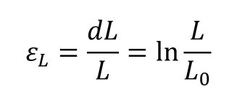 式6
式6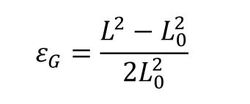 式7
式7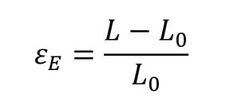 式8
式8





