非線形解析のフローと幾何学的非線形性:いまさら聞けない 非線形構造解析入門(3)(3/5 ページ)
なぜ大変形大回転を伴う計算で形状非線形性を考慮する必要があるのか
では、なぜ大きな変形や回転を伴う解析の場合には、形状非線形性を考慮しないと非現実的な結果になってしまうのでしょうか。実はこれを厳密に説明しようとすると、かなり細かく連続体力学の話を進めていく必要があり、偏微分方程式のオンパレード状態、まさに大学の授業のような内容になってしまいます。そこで以降の説明ではあくまでも概要にとどめつつ、非線形解析を実行する上で最低限必要なことだけを解説したいと思います。
このようなものの言い方には異論があるかもしれませんが、物理の理論的な意味合いでも難しい現象を解析するといったケースでなければ、商用解析ソフトで非線形問題を解析する場合に、理論の詳細を学問として理解する必要はなく、概要レベルで知識を持っていれば、まずは進められると思います。もっといえば、商用解析ソフトで大変形大回転問題を扱う場合には、「非線形」のオプションやスタディを使用する必要があるといった程度の理解で十分です。
もちろん、そうは言っても線形解析では一般的に扱わない知識が必要とはなりますので、以降で、そのあたりのお話をしていこうと思います。この後の話で重要になってくるキーワードが「ひずみ」と「応力」です。
ひずみと応力
ひずみは、並進/回転に依存しない変形の尺度です。ひずみには、この後に説明しますが、「微小ひずみ」「対数ひずみ(真ひずみ)」など異なる測度があります。
線形解析で使用するひずみ、すなわち微小ひずみを使用すると大きな回転が生じたとき、膨張するような状況が生じます。そのような問題を起こさないためのひずみの定義があります。「グリーンラグランジュひずみ」「アルマンジひずみ」などです。
連載第2回で有限要素法では、連続体力学の「Cauchy(コーシー)の第1運動法則」を解くという話をしましたが、Cauchyの応力テンソルを使ってこの方程式を導くと、非線形性が強過ぎて扱いにくいところがあります。ちなみに、現配置の微分を変形前配置での微分に書き換えると「1stピオラキルヒホッフ応力」が導かれます。ただし、この応力は非対称で扱いにくいので、対称にした「2ndピオラキルヒホッフ応力」が一般的には使用されます。
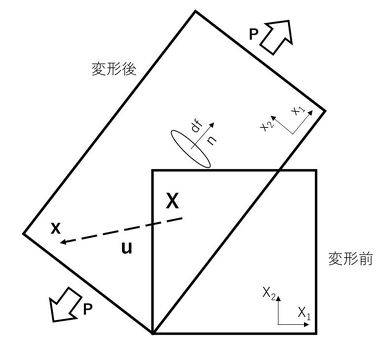
ここで一度、線形解析は何か? ということを、回転を考慮する/しないという観点から見てみましょう。以下のような正方形が回転しながら荷重で引っ張られて伸びる状況を考えてみます。
前回も説明したCauchyの第1運動法則を示します(式1)。
本来xjには、変位uが含まれています。つまり、分子と分母の双方に変位uが含まれることになり、非線形になります。ここで変位uが小さいと仮定して、xjをXjと置き換えることができます。また、ひずみを微小ひずみとすると、ひずみは以下の式で表せます(式2)。
この場合、変位uが分母には含まれなくなりますので、容易に解くことができます。要するに、線形解析ではこれを解いているということになります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

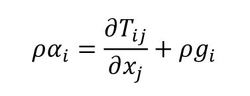 式1
式1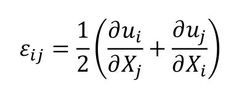 式2
式2





