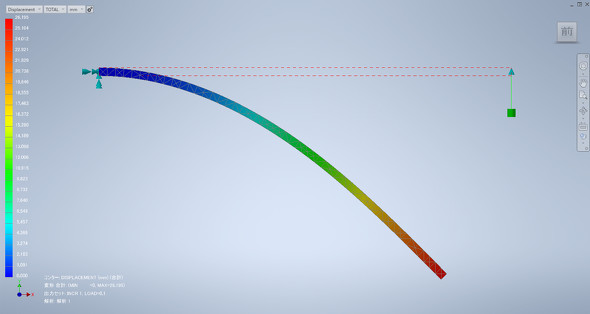
　1つ目は、「Autodesk Inventor Nastran」（以下、Inventor Nastran）で計算した片持ちはりの例です。実際にはこのように極端に曲げるということはないと思いますが、ここはあえてわざと大きくたわませてみます。本来であれば、材料は途中で塑性していると思いますが、この例では塑性のような材料非線形性は考慮しません。1×1mmの断面の長さ50mmの先端を、25mm下方向に強制変位させます。

図3　片持ちはりと境界条件（左端完全固定、右端上部に強制変位）［クリックで拡大］

　これを、形状非線形性を考慮してシミュレーションすると、図4のようになります。マイナスY方向に25mm（全長の半分）変位するとともに、マイナスのX方向にも変位しています。はりを下向きにたわませただけで全長が変わるわけではないですから当然のことですね。

図4　形状非線形を考慮している例［クリックで拡大］

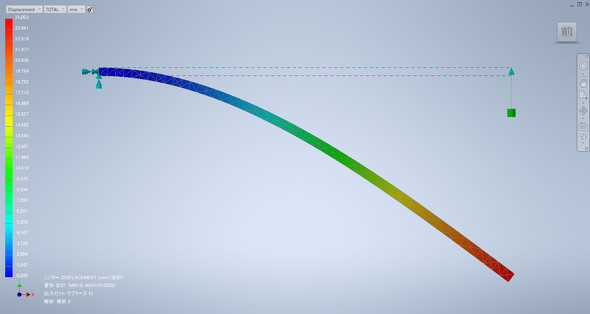
　ところが、形状非線形性を考慮しない、つまり線形の解析をすると図5のようになります。皆さんもお手持ちの線形解析ソフトで計算すると同じような結果になると思います。マイナスのY方向25mm先端が変位しているのは当然ですが、今回はX方向の変位は全くありません。つまり、真下に変位しており、はりの長さが伸びている状態となります。さらに、図5では分かりにくいかもしれませんが、はりの先端が大きく膨れています（Y方向への変位量を大きくするともっと目立ちます）。いずれにしても、現実ではありえない状況になっていることが分かります。

図5　形状非線形を考慮していない例［クリックで拡大］

例2：正方形の板の剛体回転

　もう1つ例を見てみましょう。今度は正方形の板の剛体回転です。こちらもInventor Nastranで計算しています。

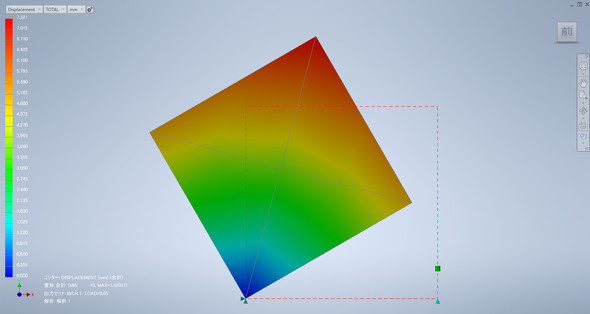
　10×10mmの板の左下の節点のみをX、Y自由度の両方を拘束してピンのように固定し、右下の節点を5mm上に強制変位させます。

図6　正方形の板の左下端固定、右下の節点を上方向に5mm強制変位［クリックで拡大］

　普通に考えて、この板は左下の節点を軸に剛体回転するはずなので、図7のようにプラスY方向に右下の節点が変位するとともに、マイナスX方向にも変位すると思われます。

図7　形状非線形を考慮している例［クリックで拡大］

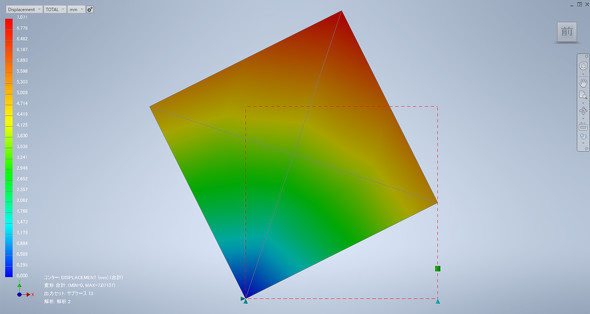
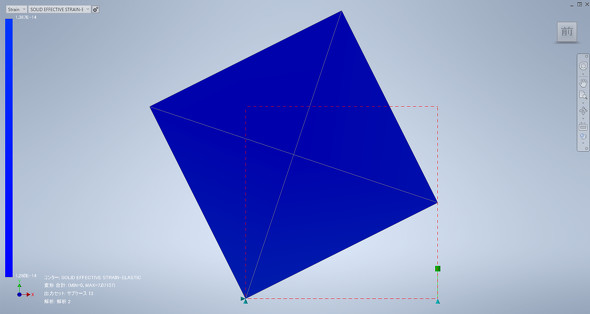
　ところが、形状非線形性を考慮しない線形解析で同じことをやると、確かにプラスのY方向に5mm強制変位するのですが、先ほどの片持ちはりと同様に、X方向に本来発生するはずの変位がありません（図8）。言ってみれば回転しながら、板自体が引っ張られて大きくなっている状態です。この例もやはり、現実の現象と違うということになります。これだけでも、おかしな状態になっていることが分かりますが、別の数値も確認してみましょう。

図8　形状非線形を考慮していない例［クリックで拡大］

　形状非線形性を考慮しない場合のひずみの大きさを見てみると、10^-14、つまりほぼ数値誤差の大きさで実質ゼロです。こんなにも板が元の大きさと比較して大きくなっているのにひずみがゼロというのは変です。しかし、そもそも剛体回転をしているだけなのでひずみがゼロというのも当たり前の話です。要するに、形状非線形を考慮せずに大回転問題を扱うと“理屈に合わない結果が出てくる”ことになります。