非線形に入る前に、線形有限要素法について復習しておく:いまさら聞けない 非線形構造解析入門(2)(1/5 ページ)
多くの3D CADではオプションとしてCAE機能が用意されているが、多くの方が「線形解析」での利用にとどまっており、「非線形解析」にまで踏み出せていない現状がある。本連載では、構造解析でも特に非線形解析にフォーカスし、初心者向けに分かりやすくその特長や活用メリットなどを紹介する。連載第2回では「非線形」の話題に入る前に、あらためて「線形有限要素法」について確認する。
連載第2回では「線形有限要素法」についてのお話をしてみたいと思います。「非線形」の連載なのに、なぜ線形? という疑問はあると思います。お話する理由は2つあります。1つは、既に解析を実践的に使ってはいても、「有限要素法」の理論的な背景について、あまりご存じない場合もあるだろうという理由。もう1つは「非線形」といっても、そのベースにあるのは「線形」なので、本格的に非線形の話を始める前に、線形について復習し、理解を深めておくべきだろうという理由です。
有限要素法(FEM:Finite Element Method)
そもそも有限要素法とは何でしょうか? そこから話を始めてみたいと思います。現在は、さまざまな物理的な挙動をコンピュータで解くことが一般的になっています。これを「シミュレーション」と呼ぶことは皆さんもよくご存じだと思います。さて、物理的な挙動をコンピュータで解くためのさまざまな手法が世の中にあります。構造物の挙動をシミュレートするために多用されている手法が、有限要素法というわけです。
では、有限要素法とはそもそも何か? ですが、簡単にいうと「解析したい対象を有限な要素に分割して、微分方程式を“近似的に”解く方法」です。もっと具体的には「Cauchy(コーシー)の第1運動法則」、あるいは平衡方程式を近似的に解くのが有限要素法です。Cauchyの第1運動法則について、より詳しく知りたい方は、連続体力学関連の書籍を読んでいただくのがよいと思います。
なお、この式1については書籍などによって、異なる形で表記されている場合もあります。
さて、解析対象が有限要素法によって挙動がどう解析されるのか、その全体的な流れをここでは確認していきたいと思います。基本的な流れをざっくり説明すると、以下の通りです。
- 離散化(メッシュ作成)
- 要素剛性マトリクスの構築
- 全体剛性マトリクスの構築
- 境界条件の適用
- マトリクスの求解(連立1次方程式を解く)
- 応力などの結果の算出
この流れは、皆さんがお使いの有限要素法の解析ソフトでしたら、基本的にはどのソフトでも同じ流れになっているはずです。ということで、これらのステップを1つずつ見ていきたいと思います。
1.離散化(メッシュ作成)
有限要素法で解析を行うためには、何はともあれ「連続体を要素に分割する」という作業が必要になります。ちなみに、連続体解析学的には、連続体とは“変位が連続であること”を意味しています。また、連続体を要素に分割することが、つまり“離散化する”ということになります。
例えば、図1のように任意の形の解析対象となる物体があるとき、これを図1右側のように分割した要素の集合体として表現することになります。
もともと連続体である領域をV、要素分割したときのそれぞれの要素の領域をVeとした場合、離散化したモデルでの全体の領域は、要素の領域の集合体となりますので、
という近似で表現することになります。
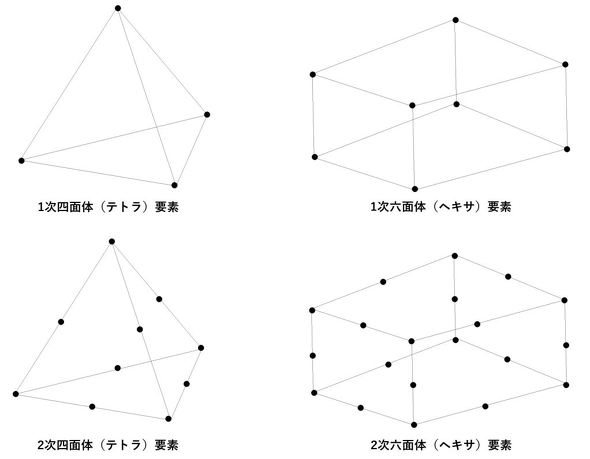
ちなみに、この離散化の際に構築される要素ですが、要素の形状は1つではありません。2次元の要素であれば一般的に三角形か四辺形、3次元の要素であれば四面体(テトラ)か、六面体(ヘキサ)のいずれかとなります。要素自体の詳細については、ここでは割愛しますが、3次元要素の場合、六面体の1次要素が、精度と計算コストの関係でいえばバランスが良く好まれるのですが(筆者もできる限り、六面体を好みます)、自動メッシュ分割が困難なため、一般的には2次のテトラ要素が選択肢(ほぼこれ一択)となるのではないでしょうか。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 超小型EV「mibot」開発に見る“制約を魅力へ変える”設計アプローチ
- 加工不備や配線不良、バッテリー不具合、熱問題 品質課題が顕在化した1月のリコール
- 製造業“現場あるある”かるた<あ行:結果発表> 秀逸作品ぞろいで審査難航!?
- 同じ機械なのに1号機はOK、2号機はNG 設計者を悩ませる“再現しない不具合”
- 【レベル9】アセンブリ図面を作成せよ!
- 新型コロナで深刻なマスク不足を3Dプリンタで解消、イグアスが3Dマスクを開発
- 3Dプリンタ製の型を活用した、回せるネジ型チョコレートの取り扱いを開始
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 【調査レポート】設計・解析業務におけるAI活用の現実と課題
- 幾何公差の基準「データム」を理解しよう

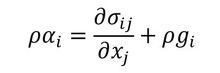 式1
式1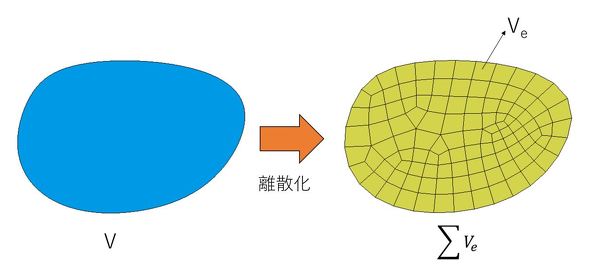
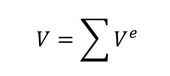 式2
式2