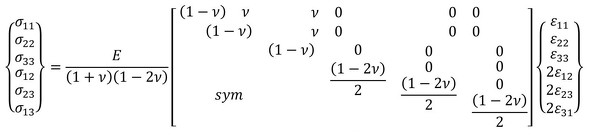非線形に入る前に、線形有限要素法について復習しておく:いまさら聞けない 非線形構造解析入門(2)(2/5 ページ)
1.離散化(メッシュ作成)の続き
さて、要素における変形は、基本的には要素を構成する変位で表現できますが、要素内部の連続性はどのように表現するのでしょうか。それは「形状関数」と呼ばれるもので、近似的に表現されています。なお、以下の式だけあっても意味がよく分からないと思いますが、ここでは形状関数というものを使うということで、その一例だとご理解ください。
- 4節点四辺形要素の形状関数(一部)
参考までに、一般的にポスト処理で応力分布などを表示するコンタープロットでは、形状関数が流用されていることがあります。また、上記の要素の処理は、全体座標系での座標を正規化座標系に転写して行われます。
2.要素剛性マトリクスの構築
メッシュが切れたということは、解析対象の形状を定義できたことになります。しかし、あくまでも“解析対象となる形状が定義できただけ”です。次に、この形状がどのような性質(硬いのか、軟らかいのかなど)を持つ材料なのかを与えてあげる必要があります。これが、要素剛性につながってくるのですが、少しその話を進めてみたいと思います。
冒頭で、Cauchyの第1運動法則を近似的に解くのが有限要素法だと説明しました。もう少し具体的に述べると、この運動法則に、応力・ひずみ関係式、形状、変位境界条件、応力境界条件を与えると、物体の変形が分かるようになります。そして、一般的に私たちが扱うような実際の部品形状は複雑な形であるため、事実上、手計算で問題を解くのは困難で、コンピュータを用い、有限要素法などで解く必要があります。
では、このCauchyの第1運動法則に与える各条件を見ていきましょう。
応力・ひずみ関係式
応力・ひずみ関係式は、いわゆる、
です。どこかで見たことのある式だと思います。ただ、この式、テンソルで表すともう少し中身が複雑になります。3次元の線形の弾性体であれば、以下のようになります。このDで示される応力と変位を関係付けるマトリクスは、しばしば「Dマトリクス」と呼ばれます。
そして、このマトリクスについて、等方性の線形弾性の材料を想定すると、物性値はヤング率(E)とポアソン比(ν)で表現できるので、式5は次の式6のように表現することが可能です。式6から、何故に解析ソフトの材料物性値において、ヤング率とポアソン比の入力が必要なのかが分かりますね。
ということで、応力とひずみの関係が分かりました。今度はひずみと変位の関係を見ていきたいと思います。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査

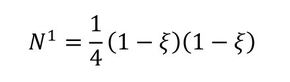 式3
式3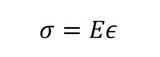 式4
式4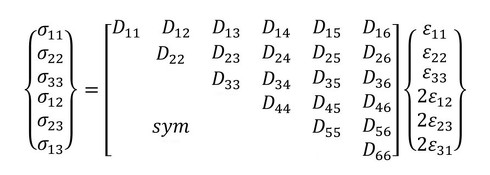 式5
式5