非線形に入る前に、線形有限要素法について復習しておく:いまさら聞けない 非線形構造解析入門(2)(4/5 ページ)
» 2022年07月04日 08時00分 公開
[水野操 mfabrica合同会社 社長/3D-GAN,MONOist]
3.全体剛性マトリクスの構築
全体剛性マトリクスは、簡単にいえば“各要素の剛性を足し合わせる”ことで構築できます。
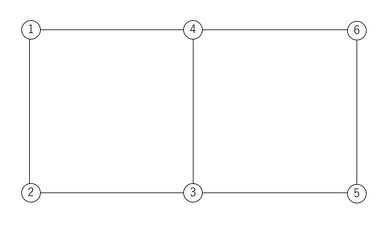
例えば、先ほどの2次元四辺形1次要素において、2要素のモデルの場合には、以下の2つの剛性マトリクスが存在します。
この2つのマトリクスを合成して、全体剛性マトリクスを構築し、変位ベクトル、荷重ベクトルとともに表現すると、以下のような式になります。
ここで、0の箇所は両方の要素からの“寄与がない”部分、足し算で表現されている箇所は両方の要素からの“寄与がある”部分となります。
4.境界条件の適用
これで問題を解く準備がほぼできましたが、まだ少し情報が足りていません。その情報というのが「境界条件」です。境界条件は、多くの解析ソフトのユーザーインタフェース上で「拘束条件」や「荷重条件」と表現されていると思います。
図5のように左辺の2節点を拘束し、右辺の2節点をある任意の荷重fで載荷することを考えるとき、これらの数値を式に組み込むと式20のようになります。なお、この際、荷重が載荷されていない(外力がかかっていない)節点の自由度に対しては、0を代入します。
この後に、変位を0とした箇所が寄与する行列を削除します。それによって、未知数の数と式の数が合うようになります。ただし、一般的に多くの商用ソフトでは、そのような教科書的な処理ではなく、別の形で処理していることが多いようです(詳しくは割愛します)。
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentsPR
Pickup ContentsPR
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
Special SitePR
あなたにおすすめの記事PR

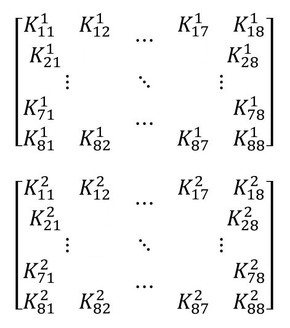 式18
式18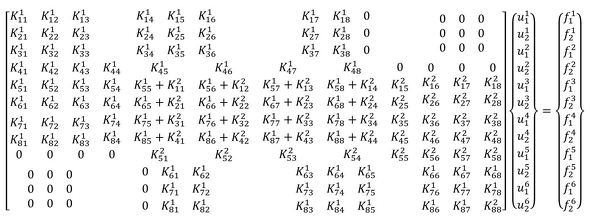
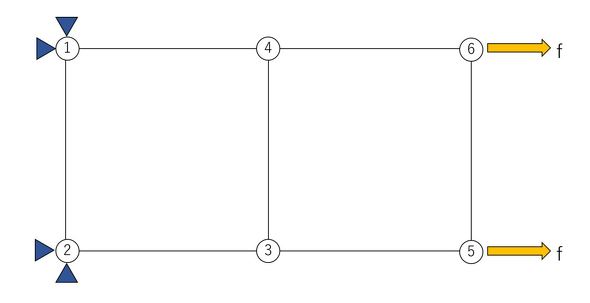
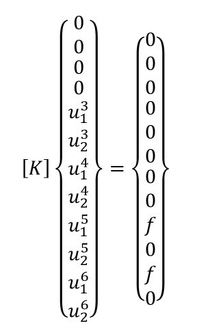 式20
式20





