非線形に入る前に、線形有限要素法について復習しておく:いまさら聞けない 非線形構造解析入門(2)(3/5 ページ)
ひずみ・変位関係式
ひずみと変位の関係は、以下のような関係で示すことができます。
ちなみに、線形の弾性解析におけるひずみは、以下の微小ひずみで表現されます。
また、変位については節点変位と形状関数を用いて、以下のように示すことができます。
これらを踏まえ、一例として、4節点四辺形要素の場合の変位とひずみは、以下のように表せます。
形状関数は要素の形状や次数に依存するため、「B」マトリクスの中身は要素の形状や次数に依存します。
では、ここからは有限要素定式化まで進みましょう。
前述のCauchyの第1運動法則を使って、物体全体の力の釣り合いを示します。
これに、仮想仕事の原理を適用すると以下のようになります。
さらに、部分積分とガウスの発散定理を使って式を変形すると次のようになります。
ここで静解析を想定すると、加速度αi=0となります。この後の詳細な式の導出は省略しますが、さらに離散化すると式14となります。
式14を前述の応力・ひずみ関係、ひずみ・変位関係、形状関数の各式を用いて整理し、なおかつ仮想変位がその式に成り立つ場合は以下のようになります。
この左辺が剛性マトリクスと変位ベクトル、右辺が外力ベクトルであるため、つまりこれは[K]{u}={f}と整理されていることが分かります。これは、連立1次方程式となるので、ある荷重に対する変位を求めることができるようになります。なお、これらの式にある積分については詳細を割愛しますが、ガウス積分などの数値積分によって行います。要素の応力やひずみは、このガウスの数値積分の都合上、「ガウスの積分点」と呼ばれるサンプリングポイントの位置で計算されます。
さて、式15の左辺の
は各要素の剛性マトリクスであり、その中身は2次元の4節点四辺形要素(1次要素)を想定すると以下の通りとなります。
この際のマトリクスの大きさは、節点数×節点の自由度数となります。通常連続体要素の場合、節点の自由度は並進自由度のみとなるので、2次元の要素であれば、XとYの2つの自由度が各節点に存在するので、この剛性マトリクスの大きさは8×8となります。
これで、要素剛性が構築できましたので、次に全体剛性マトリクスを構築することになります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング

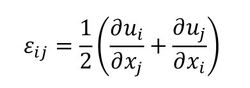 式8
式8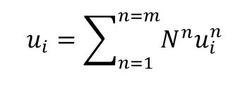 式9
式9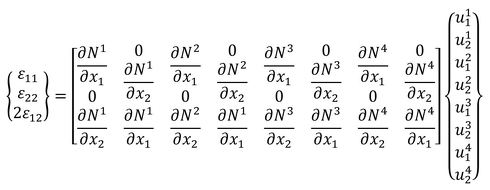
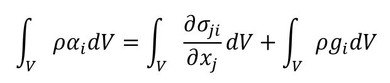 式11
式11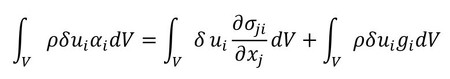 式12
式12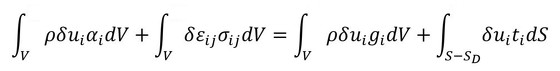 式13
式13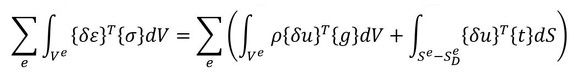 式14
式14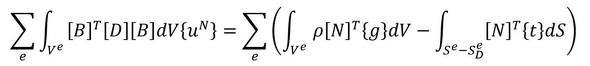 式15
式15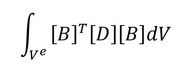 式16
式16 式17
式17





