領域最適化の基本的な考え方を理解する:フリーFEMソフトとExcelマクロで形状最適化(11)(2/5 ページ)
式2の説明
次は、式2の説明です。先に答えを述べますと、式2は「仮想仕事の原理」の式です。式5は式8と同じ形で、wは変位なのですが「仮想変位」です。式5は2次元問題なら次式で表され、仮想変位のなす仕事量です。
式2に式4を代入します。
式10左辺のvkは、荷重Pによって生じた変形量なので、その微分∂vk/∂xkはひずみです。ひずみは2階のテンソルで次式のように行列で表現できます。
eijklは、ひずみを応力に変換する作用素で、ヤング率のようなものです。4階のテンソルなので図示できません。2階のテンソルに左から4階のテンソルを掛けることで2階のテンソルが得られ、それは応力テンソルとなります。つまり、以下となります。
式10左辺の∂wi/∂xjは、仮想変位によるひずみです。これも2階のテンソルです。よって、2次元問題における式10は、上記テンソルと式9を代入して次式となります。荷重Pによるひずみと仮想変位によるひずみを区別するために、仮想変位によるひずみの頭にδを付けました。この時点でEinsteinの総和規約を使わずに普通の表記に変えています。
連載第5回で説明したように、応力とひずみの積は単位体積当たりに蓄えられる仕事量なので、式13、式14左辺は仮想変位wによって物体に蓄えられる仕事量(エネルギー)となります。右辺は前述したように仮想変位wがなす仕事なので、式15を言葉で表現すると、「1つの物体が複数の力の影響下で釣り合っているとき、その物体が十分小さい仮想変位を受けるときはその力のする仕事量は0である」ということで、仮想変位の原理となります。
少し話がそれますが、ひずみについて説明しておきます。上式のひずみεxyと材料力学のせん断ひずみγとは同じでなく、次式の関係があります。
表記を以下のように書き換えると、物体に蓄えられるエネルギーは連載第5回の式と一致しました。
式2の「subject」は、「……という条件の下で」という意味で、式15で表現される仮想変位の原理は、弾性力学の力の釣り合い式と等価なので、式2は「変位vはやたらめったに変形するのではなく、弾性力学の原理に従って決まる量であること」という意味となります。
式6を2次元問題に書き換えると次式になります。
Mは図1の変形における領域の体積ですね。よって、式3は「変形後の体積は目標体積より小さくしてください」という意味です。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査

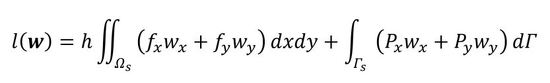 式9
式9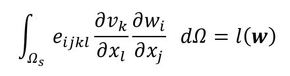 式10
式10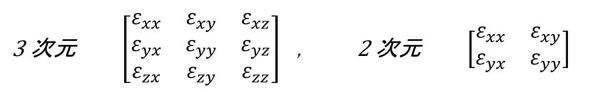 式11
式11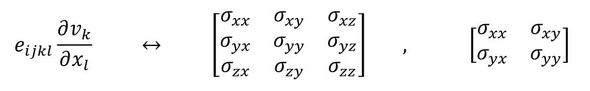 式12
式12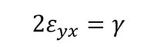 式16
式16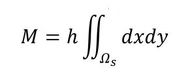 式18
式18





