領域最適化の基本的な考え方を理解する:フリーFEMソフトとExcelマクロで形状最適化(11)(1/5 ページ)
原理原則を押さえていれば、高額なソフトウェアを用意せずとも「パラメトリック最適化」「トポロジー最適化」「領域最適化」といった“形状最適化”手法を試すことができる! 本連載ではフリーのFEM(有限要素法)ソフトウェア「LISA」と「Excel」のマクロプログラムを用いた形状最適化にチャレンジする。連載第11回では、トポロジー最適化のような派手さはないが、とても実用的な技術である「領域最適化」について、その基本的な考え方を解説する。
「領域最適化」ではトポロジー(位相)は変化しません。原形状の輪郭を伸縮して、平均コンプライアンスが最小になる形状を求めます。同時に、大きな応力が発生している部分を太らせ、応力が大きくない所はしぼませて、応力が全体的に均一になるようにもします。
最大応力値は、最適化作業を進めるにつれて低減していきます。例えば、部品の形状を決めた後、強度計算をして、あと10[%]だけ応力を下げたいときなどに威力を発揮します。また、コーナーRを付け忘れて応力集中が発生している箇所に自動的にコーナーRを付けてくれます。「トポロジー最適化」のような派手さはないですが実用的な技術です。
まず、理論的な背景を説明しましょう。
領域最適化の考え方
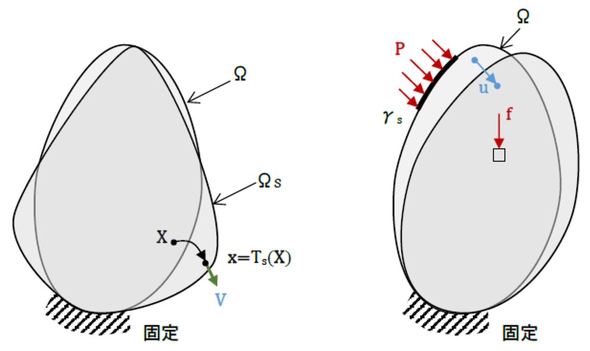
「輪郭最適化」の考え方を説明します。図1に示すように、初期領域Ωの形を変えてΩsになったとします。Ωが輪郭最適化前の領域、Ωsが最適化後の領域です。そして、図2に示すように、領域Ω(2次元物体)の輪郭の一部γsに荷重P、全体に重力などの体積力fが作用して変形したとし、ある点の変位をuとします。太字はベクトルを表しています。
剛性最大化問題、つまり平均コンプライアンス最小化問題、さらに言い換えると、物体に蓄えられるひずみエネルギー最小化問題は次式で表されます(式1、式2、式3)。
a(v,w)はひずみエネルギーを与える双一次形式、l(w)は外力によるポテンシャルエネルギー、Mは体積、Moは目標体積で、次式で表されます。これらの式は「Einsteinの総和規約」を使っています。
参考文献[1][2][3]では偏微分表示もEinstein表記をしていますが、ここでは「ライプニッツの記法」に変更しました。Einsteinが論文を書いていたころは、タイプライターを使っていたと想像しまして、偏微分記号を書くのは面倒だったと思うのですが、今は「Word」で書けるのでこうしました。
vi(次の式7に出てくる)、wiは変位、eijklは剛性です。
以上が参考文献[1][2][3]の記述ですが、翻訳しなければなりませんね。
式1のl(v)の説明を追加します。l(v)は次式で与えられ、外力によって物体を変形させたときの仕事量です。最適化に関する論文では、これを「平均コンプライアンス」と呼んでいます。この問題は、平均コンプライアンス最小化問題です。よって、式1は「物体力と外力がなす仕事量が最小になるような領域Ωsを求めてください」という意味です。
上式は2次元問題なら次式で表され、物体力fと外力Pが作用している状態で変位vがなす仕事量です。fx、fyが単位面積当たりの物体力で、例えば、重力です。3次元問題では単位体積当たりの物体力となります。2次元問題で記述したので、第1項に付いているhは板厚となります。第1項は重積分、第2項は線積分で、dΓは微小輪郭です。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

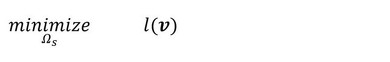 式1
式1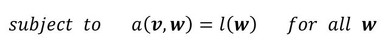 式2
式2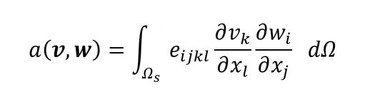 式4
式4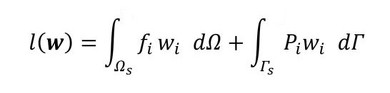 式5
式5 式6
式6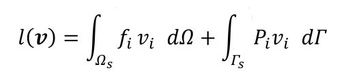 式7
式7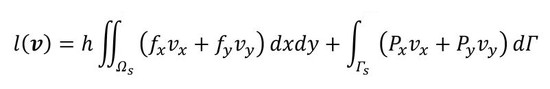 式8
式8





