領域最適化の基本的な考え方を理解する:フリーFEMソフトとExcelマクロで形状最適化(11)(4/5 ページ)
形状勾配関数 G
次はGですね。Gは、領域変動を与える速度場に対する目的関数式1の感度係数を与えるベクトル関数という意味合いを持ち、参考文献[1][2][3]では「形状勾配関数」と命名されています。
式20の第1項と第2項は変数が変わっただけで、仮想変位の原理の式なのでゼロとなって、式20に式21を代入すると次式となります。
ラグランジュ関数Lの停留条件(極値を求める条件)は次式となります。
上式が満足するような領域Ωsを求めればよいのですが、領域Ωsがスプライン曲線などでパラメトリックに定義されていればできそうですが、今回の領域Ωsはそうではないので求められそうにあません。トポロジー最適化でやったように、領域の形状を少しずつ変化させていって、ラグランジュ関数Lが最小になる形を求めていきます。繰り返し作業になります。
ラグランジュ関数の導関数が、形状勾配関数Gを係数関数とする速度場の一次形式で与えられたので、参考文献[1][2][3]で提案されている「力法(traction method)」と名付けられた方法が使えます。力法は、k回目の領域変動を表す速度場V(k)を次の支配方程式に基づいて解析する方法です。
この支配方程式を満足する領域変動Vは、凸性が保証されている問題において、ラグランジュ関数Lを必ず減少させるとのことです。ということは今回の問題は、領域の形Ωsを直接求めるのではなく、目的関数l(v)が小さくなるような形状変更の方向Vを求める問題に変わりました。毎回微小移動量Vを求めて、節点座標を移動させていくことになります。
式28は、仮想変位の原理の式と同じ形です。つまり、弾性変形問題を解けばその変位量がVとなります。式21の形は体積力fがないとした式7とそっくりです。つまり、弾性変形問題の外力はGとなります。ある条件を満たせばGは次式となるとのことですが、一番大切なこの式の導出過程を参考文献[1][2][3]から見つけることができず、文献を読んで試みたのですが筆者の力量不足で導出できませんでした……。よって、いきなり掲載することにします。うまく説明できなくて少し残念です。
この式29の第1項はひずみと応力の積です。トポロジー最適化でも使いましたね。第2項はラグランジュ乗数なのですが、体積制約式3を満足させるための調整定数として扱います。nは領域の輪郭上の外向き法線ベクトルです。
式29は平均コンプライアンス最小化から出発した剛性最大化の解を導く式です。しかし、次回以降で手を動かすと気が付くのですが、この式は「応力の大きい所を少し膨らせればよい。しかし、応力値に従って膨らませると領域表面が波打つので、弾性変形解を次世代の領域として使って、波打ちを抑える作戦」と読み取ることができます。剛性最大化と応力均一化は“お隣さん”なのだと思っています。
以上が力法の説明ですが、歯切れが悪くて申し訳ありません。しかし、結果としてこの方法が有効だったので使うことにします。
SF漫画・アニメ『銀河鉄道999』の中で、メーテルが999号のことを「遠い外宇宙の滅亡した科学惑星の遺跡や異邦人から手に入れた、まだ人類には理解できないけれど、とにかく使うことだけはできる資料を基に作られた機関車……」と説明していますが(参考文献[4])、それを聞いた気分でExcelシートを作りました。
参考文献:
- [4]松本零士|銀河鉄道999|少年画報社(S53)
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン社員が技能五輪国際大会の工業デザイン技術職種で日本代表に
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本

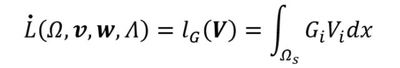 式26
式26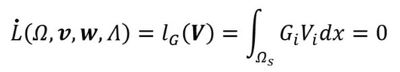 式27
式27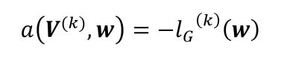 式28
式28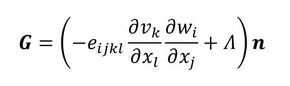 式29
式29





