領域最適化の基本的な考え方を理解する:フリーFEMソフトとExcelマクロで形状最適化(11)(3/5 ページ)
領域Ωsを求めるってどういうこと?
「物体力と外力がなす仕事量が最小になるような領域Ωsを求めてください」というのが命題でした。筆者が経験した数学は、数を求めることでした。例えば、領域をスプライン曲線で表現し、スプライン曲線のパラメータを求めるというのなら分かります。しかし、今回はパラメータなしの領域Ωsを求める問題です。さて、どうするのでしょうか。
目的関数は式1、制約関数は式2、式3なので、ラグランジュ関数Lは次式で定義できます。ここでラグランジュ乗数はwとΛとなります。
ラグランジュ関数Lを微分したものがゼロというのが「ラグランジュ未定乗数法」でした。ラグランジュ関数Lを微分したものは、参考文献[1][2][3]によると式20で示されています。本連載で、あえて使ってこなかったドット「・」(ニュートンの記法)は微分を意味し、LのEular導関数、あるいは物質導関数です。ダッシュ「’」(ラグランジュの記法)も微分を意味し、Lの形状導関数です。このあたりの詳細については、参考文献[1][2][3]を確認してみてください。
lG(V)は次式で表されます。
2つのベクトルVとGが登場しました。
図1は、初期領域Ωと変動後の領域Ωsとの1対1の写像と捉えることができて、写像Tsとして表現できます。写像の関係を次式で表現します。
媒介変数sは「変動の履歴」を表しています。領域の変動は、次のような初期条件と微分方程式を用いて表現できます。
上式は微分なので、ベクトルVは、最初の位置がXの点の移動経路(直線ではなく曲線です)が、xに至ったときの移動の方向(速度場)と解釈できます。Vは1階微分なので形式的に次式を書くこともできます。Taylor展開ですね。O(|Δs|)は微小項です。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

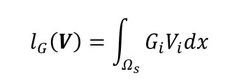 式21
式21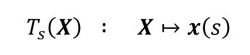 式22
式22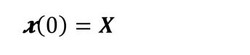 式23
式23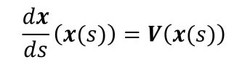 式24
式24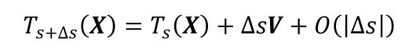 式25
式25





