トポロジー最適化 〜密度法の定式化〜:フリーFEMソフトとExcelマクロで形状最適化(5)(1/5 ページ)
原理原則を押さえていれば、高額なソフトウェアを用意せずとも「パラメトリック最適化」「トポロジー最適化」「領域最適化」といった“形状最適化”手法を試すことができる! 本連載ではフリーのFEM(有限要素法)ソフトウェア「LISA」と「Excel」のマクロプログラムを用いた形状最適化にチャレンジする。連載第5回では、トポロジー最適化における密度法の定式化に取り組む。
「トポロジー最適化」では、“剛性最大化=平均コンプライアンス最小化”を目的として、設計パラメータρiを求めます。このためには、それぞれのρiが設計対象物のコンプライアンスに大きく作用するか、ρiを変えてもコンプライアンスがほとんど変わらないか、つまり“感度”を求める必要があります。例外を除き普通の有限要素法ソフトは、個別の要素の感度を出力してくれません。どのようにして、「LISA」の出力ファイルから感度に相当するものを取り出せばよいのでしょうか。
コンプライアンスの意味
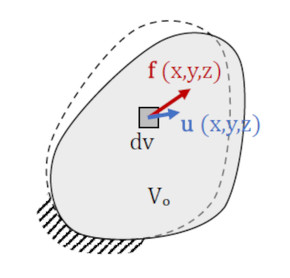
図1のように、物体に荷重f(単位体積当たりの荷重)が作用して、変位uが発生したとしましょう。荷重fと変位uはベクトル量なので太字で表記しています。
コンプライアンスの定義として、式1が挙げられます(参考文献1)。
図2に示すような2次元問題にしましょう。そして、荷重は物体表面だけに作用し、単位長さ当たりの力とします。コンプライアンスは式2となります。
式2は「平均コンプライアンス」と呼ばれています。荷重fと変位uはベクトル量なので掛け算ではなく内積として、平均コンプライアンスを荷重が作用している辺γに対する線積分で表現しています。物体を弾性体とした場合、fとuは比例関係にあるので、その内積の積分(式2の内側の積分)は図3の着色部の面積で、荷重fがなした仕事量になります。よって、式2は式3のように書くこともできます。
要するに、平均コンプライアンスは外力がなす仕事量(エネルギー)であって、最終荷重と最終変位の積の半分ということです。
「密度法」における応力とひずみの積
応力とひずみの積が何を意味しているかを考えてみましょう。図4に長さL、断面積Aの棒が荷重によってΔLだけ伸ばされた状態を示します。荷重の最終値をfとします。
引っ張られている最中、荷重fは時々刻々と増加しますが、棒は弾性体なので荷重fとuは比例関係にあり、荷重がなす仕事量(エネルギー)Wは式4で表されます。
棒に発生する応力σは、式5で表されますね。
棒の伸び量ΔLは、式6で表されます。
式5と式6を、式4に代入しましょう。
棒の体積はALなので、棒に蓄えられる単位体積当たりの仕事量は式8で表され、応力最終値とひずみ最終値の積の半分になります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 品質はどのように作られ、どのように確認されているのか
- ソフト設計者が混乱する機械屋からの要望【安全対策編/前編】
- 協働ロボット型ペレット式3Dプリンタの基本構造「バトラー方式」で特許を取得
- パナソニック コネクトがSnowflakeのAI機能を活用し、設計仕様の照合作業を9割短縮
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 超小型EV「mibot」開発に見る“制約を魅力へ変える”設計アプローチ
- 新型コロナで深刻なマスク不足を3Dプリンタで解消、イグアスが3Dマスクを開発
- 3Dプリントによる格子構造を利用した枕のクラウドファンディングを発表
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 加工不備や配線不良、バッテリー不具合、熱問題 品質課題が顕在化した1月のリコール
よく読まれている編集記者コラム

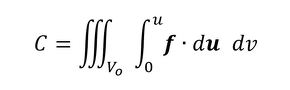 式1
式1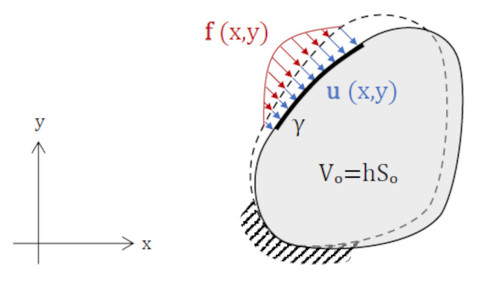
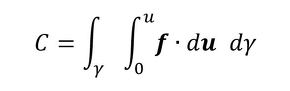 式2
式2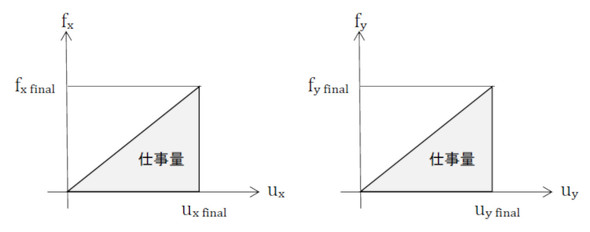
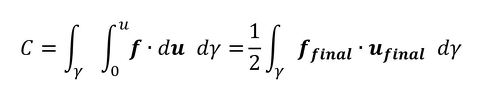 式3
式3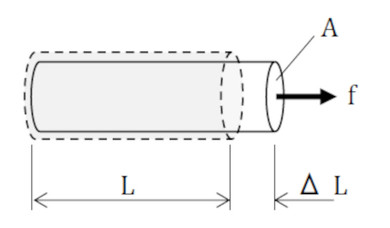
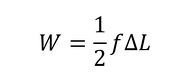 式4
式4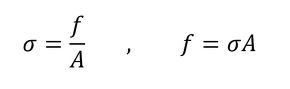 式5
式5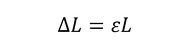 式6
式6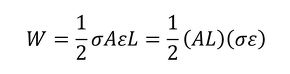 式7
式7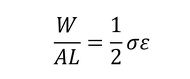 式8
式8





