トポロジー最適化 〜密度法の定式化〜:フリーFEMソフトとExcelマクロで形状最適化(5)(2/5 ページ)
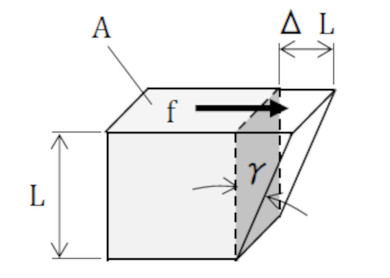
次は、せん断応力とせん断ひずみの積を考えてみましょう。図5は1辺の長さがLの立方体に、せん断荷重が作用している場合です。上から見た面積AはL2です。
立方体の上の面が荷重fを受けている最中、荷重fは時々刻々と増加することは前述したことと同じなので、荷重がなす仕事量Wは式4で表されます。
立方体に発生するせん断応力τは、式9で表されます。
立方体の上面の変位ΔLは、式10で表されます。
式9と式10を、式4に代入しましょう。
立方体の体積はL3=ALなので、立方体に蓄えられる単位体積当たりの仕事量は式12で表され、応力最終値とひずみ最終値の積の半分になります。
引張荷重とせん断荷重が同時に物体に作用したときに、物体内の微小立方体(体積Δv)に蓄えられる単位体積当たりの仕事量は式13で表されます。
ここで、hは2次元問題としたときの物体の厚さ、Δsは微小面積です。
本当はテンソルで表すべきなのですが、応力とひずみを式14のようにベクトルで表します。
単位体積当たりの仕事量は式15と表記できます。
物体全体に蓄えられる仕事量Wは、2次元問題に対しては式16で表されます。
ちょっと待ってください。密度法では少し異なります。式13は単位体積当たりの仕事量でした。一方、連載第4回で密度法は「物体が軽石のようにスカスカだ」と説明しました。式16のh dsは軽石の見掛けの体積であって、真の体積ではありません。よって、積分は「単位体積当たりの仕事量×真の体積」にしなければなりません。密度法の定義から、式16を式17のように書き換えます。
平均コンプライアンス、つまり外力がなした仕事量Cと物体全体に蓄えられる仕事量Wは等しくならなければならないため、式18が成立します。
平均コンプライアンス最小化問題は、物体に蓄えられる仕事量(エネルギー)最小化問題となり、以下のように解釈できます。
- 剛性を最大化したい
→平均コンプライアンスCを最小化したい
→物体に蓄えられる仕事量(エネルギー)Wを最小化したい
式18の左辺を使うか右辺を使うかは分かれ道です。左辺を選ぶと個々のρiの大小がCに及ぼす影響、つまり感度を求めることになり有限要素法ソフトを自作しなければなりません。一方、右辺を選ぶと個々のρiの大小がWに及ぼす影響、つまり感度を求めることは、LISAの出力ファイルからできそうです。この手で行きましょう。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

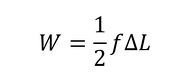 式4(再掲)
式4(再掲)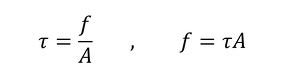 式9
式9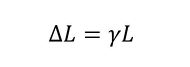 式10
式10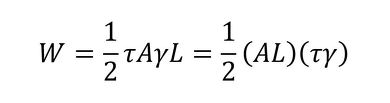 式11
式11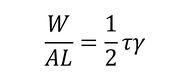 式12
式12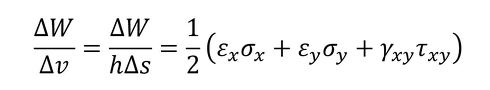 式13
式13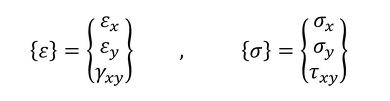 式14
式14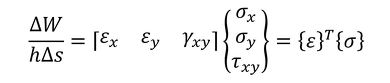 式15
式15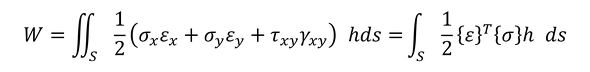 式16
式16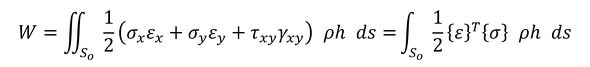 式17
式17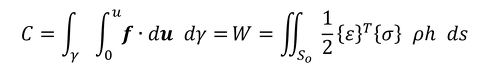 式18
式18





