トポロジー最適化 〜密度法の定式化〜:フリーFEMソフトとExcelマクロで形状最適化(5)(3/5 ページ)
物体に蓄えられる仕事量の式の変形
LISA特有の事情を考慮します。連載第1回で、「LISAの結果はテキストファイルで出力される」と述べました。応力については節点解と要素解が出力されますが、ひずみは出力されません。式17にはひずみが含まれているので、式を変形する必要があります。
連載第4回で述べたひずみと応力の関係を使います。平面応力の場合、ひずみと応力の関係は式19でした。
式19をマトリクスで表現します。
ベクトル{νσ}を式21で定義しました。
式20と式21を、式18の右辺に代入します。
{νσ}T{σ}はこれからいろいろな場面で登場します。次式で計算します。
密度法の定式化
剛性最大化問題は、物体に蓄えられる仕事量の最小化問題となり、式22が目的関数です。制約条件は「最適化後の物体の体積が元の体積Voのa倍である」とします。aは0〜1の実数です。連載第4回で話した密度の定義から、制約関数は次式となります。
目的関数、つまり物体に蓄えられる仕事量は式25となります。
目的関数を最小にする問題なので、式25を定数倍している「1/2」はなくしてしまいましょう。すると、今回の最適化問題は式26、式27で定義できます。
コンピュータは積分ができません。できることは総和をとることです。よって、式26、式27を離散化します。そして、今回の対象物は図6のような有限要素法モデルなので、対象物は要素ごとに分割されています。従って、式26と式27は次のように離散化されます。
viはi番目の要素の体積です。
式28と式29を「ラグランジュの未定乗数法」を使って解きます。ラグランジュ関数Lは式30となります。
そして、式31と式32で示す連立方程式を解けば、f(ρ1、ρ2、ρ3……ρne)が最小となるρ1、ρ2、ρ3……ρneが求まります。未知数がne+1個、式がne+1個なので、未知数が求まりそうです。
ラグランジュの未定乗数法では、極大値ないしは極小値になることを保証しているだけで、最小値になるとは限りません。目的関数の谷が複数あって、そのうちのどれか1つを探し当てるのですが、他の谷底が見つかった谷底より深いかもしれません。この点は場数を増やすことで、「多分最小である」との確信に近い感覚をつかむしかないように思えます。極大/極小になっているかどうかは、目的関数の値をモニターすれば分かります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現

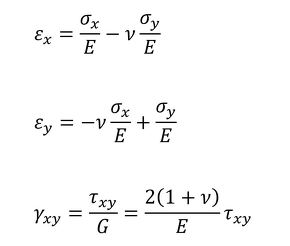 式19
式19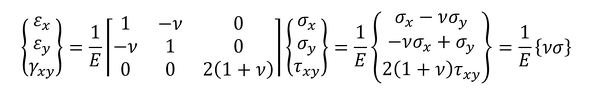 式20
式20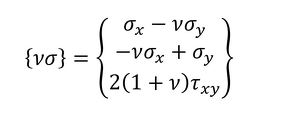 式21
式21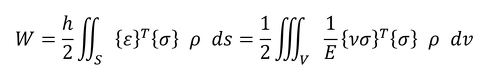 式22
式22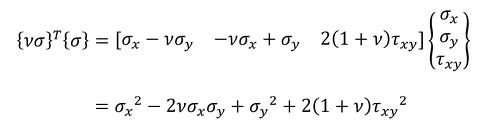 式23
式23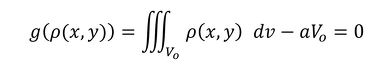 式24
式24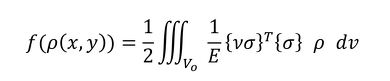 式25
式25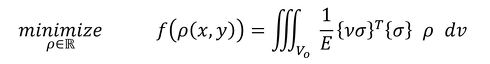 式26
式26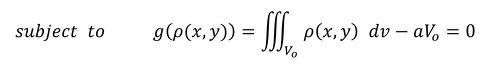 式27
式27
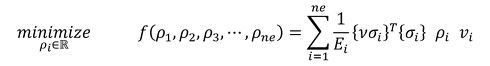 式28
式28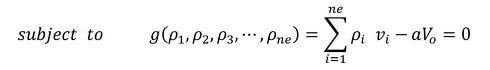 式29
式29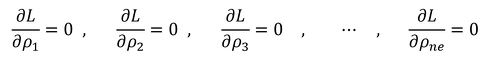 式31
式31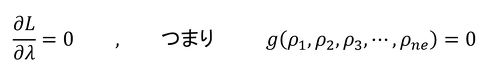 式32
式32





