トポロジー最適化に挑戦する:フリーFEMソフトとExcelマクロで形状最適化(4)(1/4 ページ)
原理原則を押さえていれば、高額なソフトウェアを用意せずとも「パラメトリック最適化」「トポロジー最適化」「領域最適化」といった“形状最適化”手法を試すことができる! 本連載ではフリーのFEM(有限要素法)ソフトウェア「LISA」と「Excel」のマクロプログラムを用いた形状最適化にチャレンジする。連載第4回では、トポロジー最適化に取り組む。
「トポロジー(位相幾何学)」は、ギリシャ語で位置を意味する「トポ」を語源としています。「トポロジーが等しい」との表現は“2つの図形の一方を伸縮すれば他方と等しい形にできる”ときに使用され、「トポロジーが異なる」との表現は“一方をどのように伸縮/変形しても他方と等しい形にできない”ときに用いられます。
「トポロジー最適化」は、何かの目標関数を最大化ないしは最小化するような形状を、トポロジーを変えることによって求める技術です。例えば、剛性最大化、平均コンプライアンス最小化、固有振動数最大化、除熱性能最大化などが目的となります。
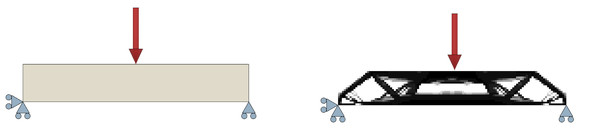
トポロジー最適化の例として、機械を軽量化したいときに“剛性をなるべく下げないで肉抜きする”ことが挙げられます。例えば、MBB(Messerschmitt-Bolkow-Blohm)はり問題では、図1のようにはりを肉抜きします。
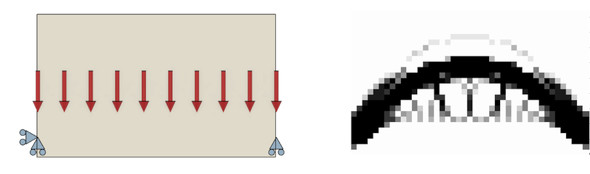
また、肉抜き問題だけでなく、形を創造することもできます。例えば、図2の左図のように、荷重と拘束点を設定すれば、白紙の状態からアーチ形状のつり橋の形を自動的に作ることが可能です。
それでは、1300節点までフリーで使える有限要素法ソフト「LISA」と、「Excel」のマクロプログラムでトポロジー最適化を行いましょう。
最適化するパラメータ
“形状を決める”ということは、「指定した空間だけに実体を詰めて、それ以外の空間を空にする」ことになります。ON/OFF問題というか0、1問題です。このようなアプローチもあるのですが、ここで紹介するトポロジー最適化は、計算過程において前述した0と1の中間的な状態を考えます。
図2の右図で灰色の領域が確認できますが、これが0と1の中間的な状態です。最終的に値は0と1だけにしますが、灰色が少し残った状態から0と1だけにする作業をプログラムでやるか、人間が判断するかは任意です。案外、全部プログラムでやってしまうと“誰がやっても同じ形”になるので、最後は設計者が判断してもよいかと思います。
0と1の中間的な状態を取り扱うので、連続的に変化する量を設計パラメータとします。つまり、トポロジー最適化も前回述べた「パラメトリック最適化」といえますので、「ラグランジュの未定乗数法」を使います。
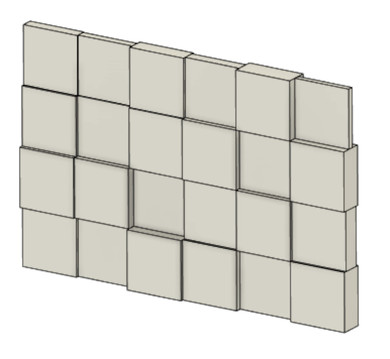
例えば、2次元問題では、板厚をパラメータとすることができます。図3のようなイメージになるでしょうか。
それぞれの要素の板厚を変化させて、剛性が最大化するような組み合わせを求めようとするものです。シェル要素を使えば、板厚を要素属性値として入力できるので使えそうです。しかし、3次元問題への拡張は諦めなければなりません。そして、難しい話になるのですが、「要素分割を細かくしたり、粗くしたりしても同じ最適解が得られるか?」との問いに答えられないそうです(参考文献[1])。
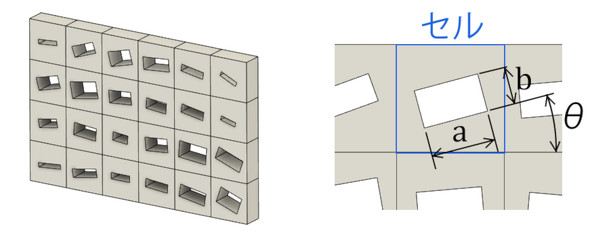
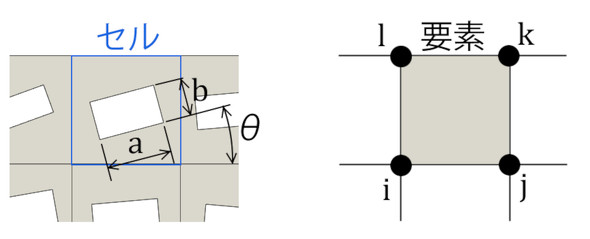
トポロジー最適化の最初の論文(参考文献[2])は図4のような発想です。それぞれのセルに長方形の穴が開いていて、穴はその寸法a、bと傾き角θで定義されます。セルの剛性と体積は穴の寸法で表現します。セルの穴が大きいほどセルの剛性が低くなります。
有限要素法解析では、図5のように“1つのセルを1つの要素”とします。つまり、穴があっても剛性が等価な1つの要素を導入します。等価的な剛性マトリクスの各成分は穴の分だけ小さくなります。また、縦方向と横方向で剛性が違うので異方性を考慮した剛性マトリクスとなります。この方法は「均質化法」と呼ばれています。2次元問題では、剛性マトリクスは式1のようになります。
{f}は荷重ベクトル、{δ}は変位ベクトルです。本連載ではマトリクスの計算式で、n行1列のマトリクスはかっこ記号{ }を、n行m列のマトリクスはかっこ記号[ ]を使うことにします。
均質化法を行うには、自分で有限要素法プログラムを作らねばなりません。そして、等価剛性マトリクスの各成分をa、b、θの関数で表す必要があります。この作業は、a、b、θを数段階に離散化し、セルを要素分割して有限要素法で求めることで行えそうですが、かなりの作業量になりますね。
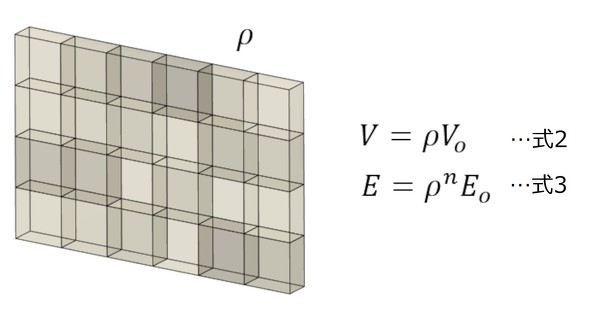
次に紹介するのは「密度法」(参考文献[3])です。少し分かりにくいのですが図6のようなイメージです。それぞれの要素には“スカスカ度合い(密度)がある”という発想です。軽石のようなイメージでしょうか。
要素がスカスカな場合、実のある部分の体積は見掛けの体積よりも小さくなるので、密度ρを導入して式2のように体積を定義できます。Voは見掛けの要素の体積です。式3は要素のヤング率で、Eoはスカスカでない場合(ρ=1)のヤング率となります。Eはスカスカな場合のヤング率です。nは任意の実数なので、1〜3でよいでしょう。ρが設計パラメータとなります。そして、式3を利用すると市販の有限要素法プログラムを利用でき、自分で有限要素法プログラムを作る必要がなくなります。また、3次元への拡張も容易です。
本連載のトポロジー最適化では、密度法を使うことにします。
参考文献:
- [1]菊池昇/均質化法による最適設計理論/応用数理 VOL.3 NO.1(1993)
- [2]Bendsøe,M.P.and Kikuchi,N.:Generating optimal topologies in structural design using a homogenization method,COMPUTER METHODS IN APPLIED MECHANICS AND ENGINEERING 71(1988)197-224
- [3]M.P.Bendsøe,Optimal shape design as a material distribution problem,Structural Optimization, VOL.1 No.4 pp.193-202(1989)
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 品質はどのように作られ、どのように確認されているのか
- 加工不備や配線不良、バッテリー不具合、熱問題 品質課題が顕在化した1月のリコール
- ソフト設計者が混乱する機械屋からの要望【安全対策編/前編】
- パナソニック コネクトがSnowflakeのAI機能を活用し、設計仕様の照合作業を9割短縮
- 新型コロナで深刻なマスク不足を3Dプリンタで解消、イグアスが3Dマスクを開発
- 超小型EV「mibot」開発に見る“制約を魅力へ変える”設計アプローチ
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 3Dプリントによる格子構造を利用した枕のクラウドファンディングを発表
- 幾何公差の基準「データム」を理解しよう
- 3σと不良品発生の確率を予測する「標準正規分布表」

 式1
式1