トポロジー最適化に挑戦する:フリーFEMソフトとExcelマクロで形状最適化(4)(3/4 ページ)
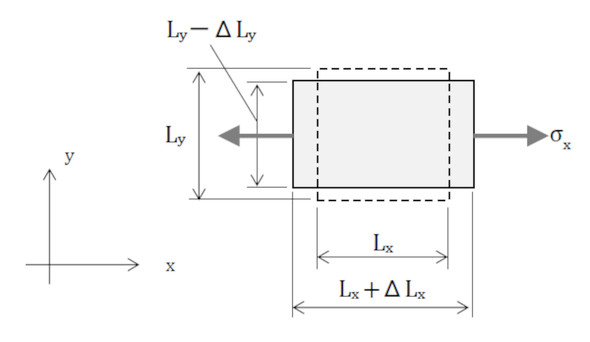
応力−ひずみマトリクス[D]は重要なので導出しましょう。材料力学のポアソン比の定義を思い出してください。図9に微小四角形をx方向に引っ張った場合を示します。微小四角形はx方向にΔLxだけ伸び、y方向はΔLyだけ縮みます。x方向ひずみをεx、y方向ひずみをεyとすると、εyとεxの比がポアソン比でしたね。εyとεxの符号が異なるため、ポアソン比νは式14で定義されています。
微小四角形をx方向とy方向同時に引っ張った(引張荷重が作用した)場合を考えます(図10)。σxによりx方向にεx=σx/Eのひずみが発生し、同時にy方向にεy=−νεx=−ν(σx/E)のひずみが生じます。Eはヤング率です。一方、σyによりy方向にεy=σy/Eのひずみが発生し、同時にx方向にεx=−νεy=−ν(σy/E)のひずみが生じます。両者を重ね合わせると、式15ができます。
式15から、σxとσyを求めます。次式となります。
ついでに、せん断応力とせん断ひずみγxyの関係も考慮しましょう(式17)。
式16と式17を一緒にしてマトリクス表記すると、応力−ひずみ関係式と応力−ひずみマトリクス[D]は次式になります。
式18には係数E/(1−ν2)がかかっています。これを取り出しましょう。次式になります。
では、剛性マトリクスはどうなるのでしょうか。式5の重積分は、要素の面積分です。2次元三角形1次要素の場合、剛性マトリクスは積分が簡単になって次式となります。Sは要素の面積です。
式20に式19を代入します(式21)。
式21を見ると、最適化の対象となるパラメータは、板厚hとヤング率Eとなります。hをパラメータとすると板厚最適化となり、Eをパラメータとすると密度法となります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

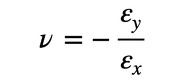 式14
式14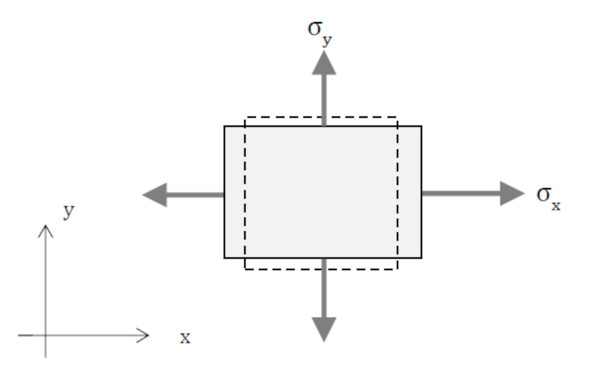
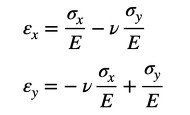 式15
式15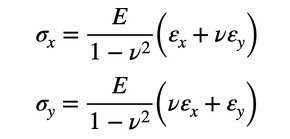 式16
式16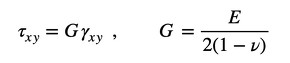 式17
式17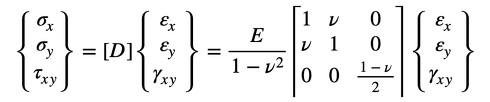 式18
式18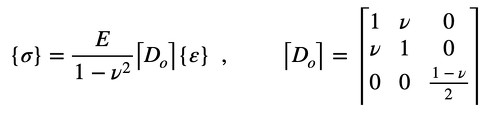 式19
式19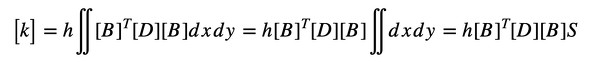 式20
式20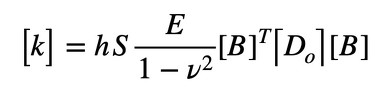 式21
式21





