トポロジー最適化に挑戦する:フリーFEMソフトとExcelマクロで形状最適化(4)(2/4 ページ)
密度法と有限要素法
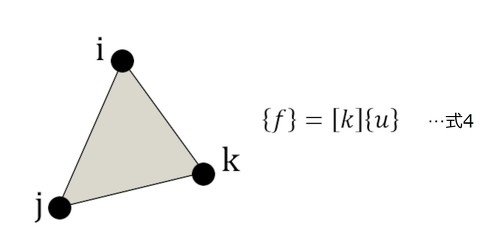
密度法を採用したときの有限要素法プログラムの活用方法について解説します。話を簡単にするために、平面応力問題とし、図7のような2次元三角形要素の剛性マトリクスで説明します。{f}は荷重ベクトル、{u}は変位ベクトル、[k]は剛性マトリクスです。
2次元問題の場合、剛性マトリクス[k]は式5で計算できます。なお、式5の導出は参考文献[4]のWebサイトが参考になります。hは要素の板厚です。
各節点(i,j,k)に変位があって、その変位量が一致していない場合は要素が引き延ばされているので“ひずみ”が発生します。よって、ひずみは変位ベクトル{u}で決まることになり、その関係は式6、式7で表されます。{ε}はひずみ、{u}は変位ベクトルです。[B]は変位−ひずみマトリクスといい、3行6列のマトリクスです。変位−ひずみマトリクス[B]は要素の形状で決まります。
ひずみと応力は、図8に示すように「x軸を法線とする面に、x軸方向に作用するひずみをεxx、応力をσxxと表記し、x軸を法線とする面に、y軸方向に作用するひずみをεxy、応力をσxyと表記する」ことが正確な表現です。添え字が「x面を法線とする面」と「x軸方向に作用する応力」というように2つあるので、ひずみと応力はテンソル量として2行2列のマトリクスで表現されます。しかし、有限要素法ソフトではこれをベクトル量として表現してプログラミングされています。よって式7において、ひずみをベクトル量として表記しました。
また、式8の関係があって、2種類あったせん断ひずみとせん断応力は1つの量として表されます。
材料力学で述べられているせん断ひずみγxyと図8で述べたせん断ひずみεxyは少し違っていて、式9にその関係を示しておきます。
ひずみの表記を式10のように変更すると、ひずみは式7のようになります。
応力の表記も式11に変更し、応力もベクトル量として表記します。
式5の[D]は応力−ひずみマトリクスで、3行3列のマトリクスです。応力とひずみの関係は次式で表されます。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現

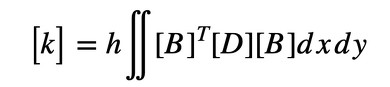 式5
式5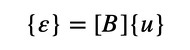 式6
式6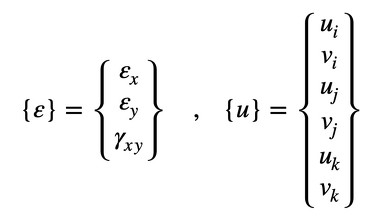 式7
式7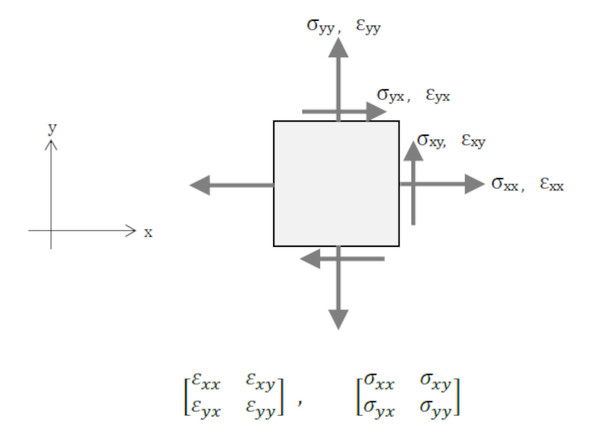
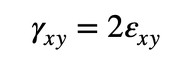 式9
式9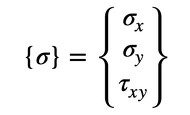 式12
式12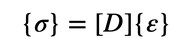 式13
式13





