トポロジー最適化 〜密度法の定式化〜:フリーFEMソフトとExcelマクロで形状最適化(5)(4/5 ページ)
密度ρiの導入と有限要素法ソフト「LISA」との相性
密度法ではヤング率を次式で定義します。添字iはi番目の要素という意味です。密度が小さいとヤング率も小さくなり、密度が1のときヤング率は元の材料のヤング率Eoに等しくなります。これをラグランジュの未定乗数法による式に導入しましょう。
上式のヤング率を有限要素法ソフトに入力したときの、ひずみと応力がどうなるかを考察します。ここでは話を簡単にするため、図7に示す平面応力三角形要素を使います。
荷重ベクトル{fi}、変位ベクトル{ui}とそれらを関連付ける剛性マトリクス[ki]を以下に示します。ここでのiは図7のi節点ではなく要素番号です。
連載第4回の剛性マトリクスの式を以下に示します。
式33から、素材のヤング率はEo、それぞれの要素の最適化後のヤング率はEiなので、ヤング率Eoを使った剛性マトリクス[ki(Eo)]は式37、ヤング率Eiを使った剛性マトリクス[ki(Ei)]は式38となります。
ヤング率としてEoを使った場合と、Eiを使った場合のひずみを比較してみましょう。まず、Eoを使った場合です。式35を左から[ki(Eo)]−1を掛けます。肩の「−1」は逆マトリクスを意味します。
変位ベクトルからひずみを求めます。連載第4回で出てきた、変位−ひずみマトリクス[B]を使います。
今度は、Eiを使った場合です。式35を左から[ki(E)]−1を掛けます。
そして、式38を代入します。
変位−ひずみマトリクス[B]は、要素の形状で決まるのでヤング率が変わっても変化はありません。Eiを使った場合のひずみは次式となります。
ヤング率Ei=ρinEoを使った場合、ひずみはヤング率Eoを使った場合の「1/ρin」倍になります。ρiは0〜1の実数なのでひずみは大きくなります。そりゃそうですね。ヤング率が小さくなったら変形は大きくなって、ひずみも大きくなります。
応力はどうでしょうか。調べてみましょう。連載第4回で出てきた応力−ひずみマトリクス[D]を使います。ヤング率がEoの場合の応力は式44で表されます。
ヤング率がEiの場合は以下となります。
式43を代入しましょう。
式44と式46は等しくなりました。応力はヤング率が変わっても変化はありません。静定はりの曲げモーメントは形状と荷重だけで決まるので、ヤング率が変わっても曲げ応力は変わらないのと同じですね。
ヤング率を変えても応力が変わらない性質を利用しましょう。有限要素法ソフトLISAが出力する応力値を使って密度法で最適化問題を解くとき、式33で示したようにヤング率をいろいろと変化させるのですが、ヤング率を変えても目的関数の元となる応力値は変わりません。よって、LISAが出力する応力値をそのまま使うことができます。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

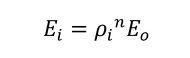 式33
式33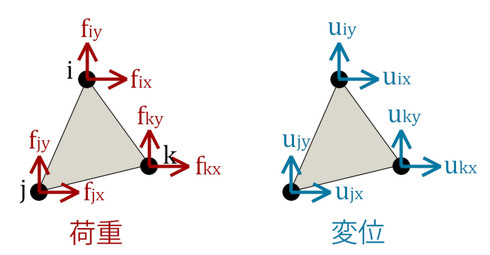
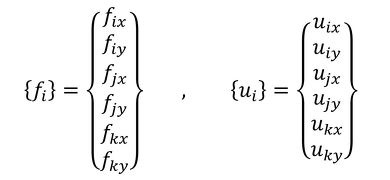 式34
式34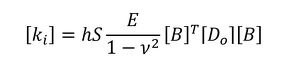 式36
式36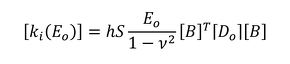 式37
式37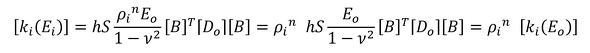 式38
式38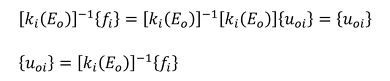 式39
式39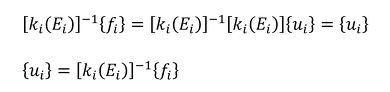 式41
式41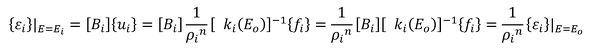 式43
式43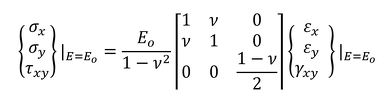 式44
式44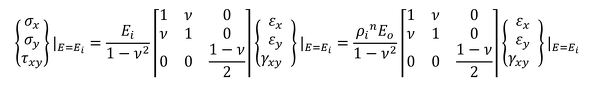 式45
式45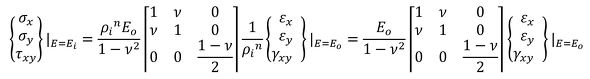 式46
式46





