公差を緩くすればコストダウンできるわけではない:3D設計推進者の眼(27)(3/3 ページ)
統計学的に考える
では、これに“統計学的”な考え方を取り入れた場合は、どのようになるのでしょうか。統計学的に考える場合には、“正規分布”を考えます。
“正規分布”の詳細については、次の機会にお話しします。また上図は再び登場します。ここでは、“正規分布”でバラツキを考えた場合、「必ずしもワーストケースにはならない」ということでお話を進めていきます。
すなわち、±0.1[mm]と寸法公差が設定された部品は、必ずしも最大値+0.1[mm]、最小値−0.1[mm]として存在することは、“統計学的”には考えられないということになります。
この場合は、下記のように計算を行います。
この計算を「不完全互換性の方法」「√(ルート)計算」と呼びます。この不完全互換性の方法からいえることは、±0.1[mm]の寸法公差値によって設定された部品では、“正規分布±3σ”においては、99.7%の確率で、10±0.22[mm]の値に収まるということになります。また、不完全互換性の方法では、互換性の方法と異なり、ここの例では部品を入れ替えた場合、完全な互換性がないことも示しています。
注意としては、この不完全互換性の方法を使用するには、その構成部品は“正規分布”の状態にあることが条件ですので注意しなければなりません。統計学的に考えているのであれば、ある確率において良品と不良品が存在しているという考え方に基づいていることになります。
「互換性の方式」と「不完全互換性の方法」を比べてみると、同じ公差が設定された部品にもかかわらず、その組み立て後の公差値が、互換性の方法が不完全互換性の方法よりも大きなことが分かります。
ここまででは、部品に設定された公差値から組み立て後の製品の公差値を求めましたが、逆に組み立て後の公差値を決めた後で、どのように部品に対して部品を設定するのかという見方をしてみます。
先ほどの部品と同じ形状で、組み立て後の公差値を±5[mm]を満足するような部品への寸法公差を、互換性の方法と不完全互換性の方法で計算してみましょう。
完全互換性の方法
部品の寸法公差をAとします。
不完全互換性の方法
部品の寸法公差をBとします。
先ほどの製品の結果と同じになることは当然なのですが、見方を変えることで、同じ組み立て後の公差を満足する上では、不完全互換性の方法を取ることにより、寸法公差は緩くできるということが理解できると思います。
しかし、注意事項として、不完全互換性の方法は、構成部品が正規分布にあることを条件としました。“正規分布”のデータを得るには、大量な部品製作におけるデータ取りが必要になるため、不完全互換性の方法は量産向きであることが言えます。
では、私のように大量生産を行わず、必要な時に必要な数のみを個別受注生産するような企業においては、この不完全互換性の方法は当てはまるのでしょうか。このような条件下で同じ部品を製作する場合には、“統計学的”に“一様分布”を考えます。
この“一様分布”も先ほどの“正規分布”同様に改めてお話ししますが、下図のような考えに基づきます。
個別受注生産型企業で、受注ごと製作される部品もある正規分布を取りながら、上図で言うU(アッパーリミット)、L(ロワーリミット)の中に存在するという考え方ができるというものが、“一様分布”にあるということになります。
そのような製品の場合、加工する人は加工図面の公差に入れるように努力します。結果その公差値に収まるわけですが、その製作の都度、その中心値は異なる可能性があります。そのようなことから“正規分布”を取りながら、“ある区分”すなわち許容値の中を移動しているという考え方が成り立つわけです。
次回も“統計学的な”お話を続けたいと思います。(次回に続く)
関連記事
 「実機レスによりデバッグ完了期間が1週間短縮」は大きいといえるのか
「実機レスによりデバッグ完了期間が1週間短縮」は大きいといえるのか
機械メーカーで3D CAD運用や公差設計/解析を推進する筆者から見た製造業やメカ設計の現場とは。今回は、フロントローディングとはどういうことなのか、実機レスデバッグの試算例も見ながら考えてみる。 設計者によるPDM導入で大事なフォルダ構成検討
設計者によるPDM導入で大事なフォルダ構成検討
機械メーカーで3次元CAD運用や公差設計/解析を推進する筆者から見た製造業やメカ設計の現場とは。今回は設計者のためのPDMにおける構造について説明する。 開発・デバッグ作業を楽にするFPGA開発環境
開発・デバッグ作業を楽にするFPGA開発環境
前回に引き続き、FPGAの開発環境について解説。FPGAは実機検証ができるだけがメリットではなく、デバッグを楽にしてくれる大きな利点もある KGDBを使って、Android組み込みボードをリモートデバッグしよう!【前編】〜KGDBの仕組みを理解する〜
KGDBを使って、Android組み込みボードをリモートデバッグしよう!【前編】〜KGDBの仕組みを理解する〜
「AndroidのUSB機能」をテーマに、Android搭載の組み込みボードを実際に用いながら、その仕組みなどについて詳しく解説する連載。第2回となる今回は、Linuxカーネルデバッガ「KGDB」の仕組みについて詳しく解説する。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
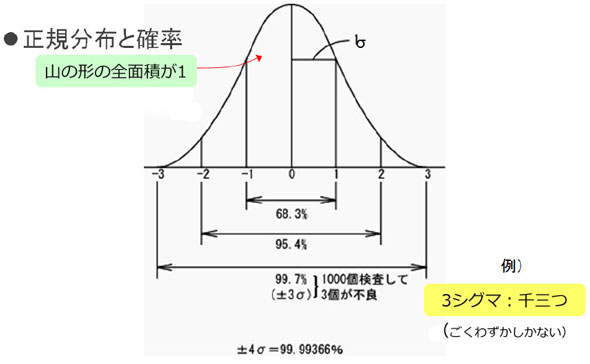 正規分布と確率:SWWJ2017東京にて使用の資料から正規分布について抜粋(講演者:筆者、出典元 PLANER)
正規分布と確率:SWWJ2017東京にて使用の資料から正規分布について抜粋(講演者:筆者、出典元 PLANER)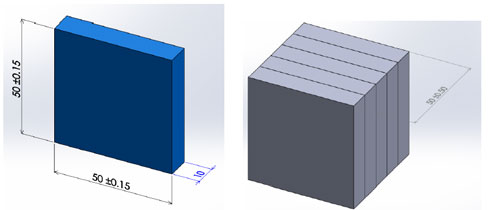
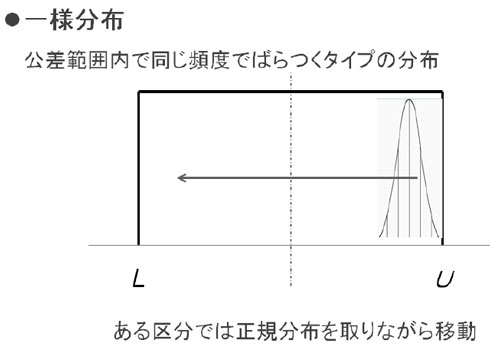 SWWJ2017東京にて使用の資料から一様分布について抜粋(講演者:筆者)
SWWJ2017東京にて使用の資料から一様分布について抜粋(講演者:筆者)






