構造物破壊の一要因にもなるカルマン渦の解析:無償ソフトで流体解析(3)(3/3 ページ)
また、渦の発生は圧力の変化を伴うため、渦の発生により音を発生させます。これが「エオルス音」と呼ばれる現象で、電線が風によりうなり音を生じるのはこのためです。渦の発生周期が構造物の共振周波数と一致して、構造物を破壊させることもあります。1940年にアメリカで発生したタコマナローズ橋の崩落事故は、横風により発生したカルマン渦と橋の共振周波数が重なったことが原因とされています(関連リンク:タコマナローズ橋(ウィキペディア))。
訂正情報(2025年8月12日):記事公開時点で、高速増殖炉「もんじゅ」のナトリウム漏えい事故について、「カルマン渦」がさや管を振動させて生じた疲労破壊が原因としていましたが、読者から事実とは異なるとの指摘を受け削除いたしました。実際には、交互渦と対称渦による抗力方向の振動に起因する破損が原因となります。
※参考文献:「配管の設計解析法」(著:水野貞男)第7.4章 P339〜345
もし、カルマン渦の発生周期が計算で求められれば、設計段階でこうした事故を未然に防ぐことができそうです。実は、計算することが可能で、下記の「ストローハル数」と呼ばれる無次元数を用います。
ストローハル数Stは下記の式で定義される無次元数で、空気ではおおむね0.2になります。
ここで、fはカルマン渦の発生周期[Hz]、Dは代表長さ[m]、Uは主流の流速[m/s]です。空気のストローハル数は0.2として、カルマン渦の発生周期は下記の式で求められます。
今回のシミュレーション条件から、カルマン渦の発生周期を計算し、画像ファイルから同じパターンとなる周期を読み取り、比較してみます。今回のシミュレーション条件では流速が5m/sで、円柱の直径は35mmです(解析領域の長さが0.5mで、境界条件を示すbc.bmpの横幅は128ピクセルで、円柱の直径は9ピクセルから0.5*9/128=0.035m)。以上を(2)式に代入すると、f=28Hzとなり、1/28=35msごとに同じ状態となることが分かります。一方、figsフォルダ内の画像を比較すると、9700サイクルと10000サイクルとがほぼ同じ状態となっていることが分かります。画像の右下にt=〜として、実際の時間が表示されているので、10000サイクルと9700サイクルの時間差を計算すると、30msと、(2)式で計算した結果とほぼ一致することが分かります。このように、カルマン渦の発生周期を求めることは設計以外にも、シミュレーション結果をより良く表すために、出力タイミングを適切に設定する際にも必要となります(関連リンク:ストローハル数(ウィキペディア))。
では、円柱の形状を変化させたら、カルマン渦の発生状況がどのように変わるか、Flowsquareでシミュレートしてみます。円柱に後方に向けて「ひれ」を付けた形状で解析した結果を用意しましたので、karman_2.zipをダウンロードして展開してください。
Flowsquareを起動し、Karman_2を解析モードで開くと、シミュレーション結果が見られます。円柱周りの流れと同じ出力タイミングの画像を図3と図4に示します。
対応する図1、図2と比べると、渦の発生位置は、より後方で狭い幅になっていることが分かります。
前述のように、渦の放出により円柱は反作用を受けるため、ひれ付円柱では、渦から受ける反作用は小さく、かつ変動も小さいことが分かります(以下の動画)。
次回は、境界条件の設定方法について説明します。また、解析事例として、翼周りの流れをシミュレートし、揚力の発生する仕組みを見てみます。
筆者紹介
伊藤孝宏(いとう・たかひろ)
1960年生。小型モーターメーカーのエンジニア。博士(工学)。専門は流体工学、音・振動工学。現在は、LabVIEWを使って、音不良の計測・診断ソフト、特性自動検査装置などの開発を行っている。
関連記事
 無償ソフトで3次元構造解析をしよう(前編)
無償ソフトで3次元構造解析をしよう(前編)
無償で使えて、要素数や利用期間に制約もない「Adventure_On_Windows」で構造解析をしてみよう! 今回は、「インストール編」。 無償ソフトで3次元構造解析をしよう(後編)
無償ソフトで3次元構造解析をしよう(後編)
無償で使えて、要素数や利用期間に制約もない「Adventure_On_Windows」で構造解析をしてみよう! 今回は、「モデリング&解析実践編」。 無償の工学計算ソフト「FreeMat」をインストールしよう
無償の工学計算ソフト「FreeMat」をインストールしよう
無償の工学計算ソフトでも、かなり高度な計算ができる! 今回はインストール編。工学計算の初心者もぜひチャレンジしよう。 オープンソースの無償3D CAD「FreeCAD」を使ってみた
オープンソースの無償3D CAD「FreeCAD」を使ってみた
ユーザー登録不要の無償CAD「FreeCAD」はモデリング以外の機能も盛りだくさん。一度覚えたら、今後のモノづくりの世界がぐっと広がること請け合いだ。今回はモデリング機能の一部を紹介する。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
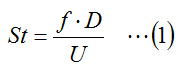

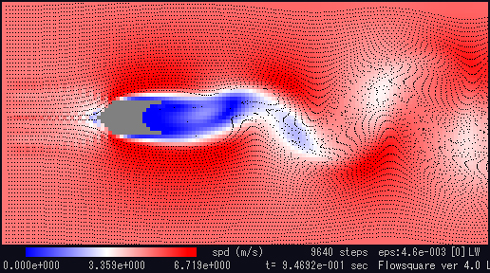 図3:ひれ付円柱周りの流れ(0.95秒)
図3:ひれ付円柱周りの流れ(0.95秒)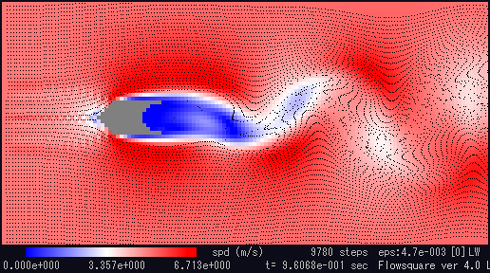 図4:ひれ付円柱周りの流れ(0.96秒)
図4:ひれ付円柱周りの流れ(0.96秒) ,/mn/subtop/features/freetools/index.html
,/mn/subtop/features/freetools/index.html





