公差解析の基本おさらいタイム始まるよ:公差解析 基本中の基本(8)(3/3 ページ)
Excelで公差計算シートを作る
よしきた。こんな感じで枠を作って……と。
入れられるところは入れていきましょー。
よし、次は係数じゃな。テーブルの「受け面高さ」とピンの「測定面高さ」は1、と。あとのはちと考えないといかんなぁ。
これは二段階で考えた方がよさそうだね。まず、「穴位置−1」の高さが1mm上がったとき、テーブルの中心の高さは幾つ上がるかな……。
ちょうど半分だから0.5mmですぅ。
ありがとう、ココちゃん。じゃあ次はピンの高さ、と。「穴位置-1」の方のテーブルの高さが、いま0.5mm上がっています。このとき、ピンの高さは幾つ上がるかな?
それは0.35mmになるね!
ありがとう、この“0.35”が「穴位置−1」の係数だね。
ちょっとひと手間掛かるねぇ。うっかり忘れそうだな。
「穴位置−2」も考え方は同じだから、係数は“0.35”ね。じゃあ「穴位置−3」と「穴位置−4」は?
さっきの考え方を逆にすればいいんじゃないかな。テーブルの高さのところは同じだから、ステップ2のピンの高さを考えるときに、高さを上げるポイントを逆にするんだね。
なるほど〜。じゃあ、0.15mmだね。お腹空いたなぁ。
あとはテーブルの「穴位置−A」と「幅位置」だね!これはステップ2の考え方を流用しちゃおう! 今度はテーブルの穴と幅の位置が、それぞれ1mm高くなった場合だね。
そうすると今度はテーブルが下がるのぅ。ピンの位置は「穴位置−A」が1mm上がると、0.7mm下がる、「幅位置」が1mm上がると0.3mm下がるな。
よし、ここまでのシートはこうなるわね。
ユーたち! 4σのバラツキになっている「測定面高さ」の係数忘れてるYO!
おぉぉ。忘れてた! 今回は3σで二乗和平方根を出したいから……係数は0.75にしないとね。よし……これで……で〜きたぁ〜!
二乗和平方根の結果が±0.1を超えてるわね。
ホントだ! こんなときのための公差寄与度ですな。おっ、ピンの「測定面高さ」とテーブルの「穴位置−A」が要チェックだね。
ピンの測定面の高さは、0.05にするのはどうかな。
あと、テーブルの「穴位置-A」の位置度をφ0.2からφ1.5にしてみる?
じゃあ、公差計算シートに数値を入れ直して……と。
やったー! ±0.1に入るね!!
あとは、今回は寄与度だけを見て数値を変えたけど、実際は現実的にできる個所と数値を相談しながら決めないといけないね。
でも皆で1つ、結果が出たね! これ、実はオジイたちが昔、係数とバラツキの考え方を含まないで計算した問題だったんだよ。ほら。
オジイたちも大胆だねぇ〜。ビシビシに厳しくしちゃってるよ!
ホントね。これじゃあ、量産したらも想定外にバラツキが小さくなるわね。改善案をちゃんと計算すると、±0.07だもん。
昔のワタシもそうだったが、気を付けないといかんなぁ。
ひとまずこれにて解決! さ、温泉に入ろう〜。
キューッと一杯♪ ルンルン♪
オジイからのお題も解決したご一行は、無事ハコ根のお風呂を満喫しましたとさ。めでたしめでたし。
ここまでのおさらい
今回は第1〜7回のおさらいとして、オジイからのお題を解決していきました。今回は、ケースの穴位置に対する係数の出し方に、ちょっとひとひねり入りましたが、これはいろいろなタイプの製品で見られるパターンです。
ステップも2つ、3つと部品の構成によって増えてきます。こんなとき、間違いがないようにするにはどうすればいいか……? やはり基礎に忠実に、ポンチ絵や部品のつながりを作ることで問題を整理するのが一番です。そして、場数をこなして経験を積んでいってください。
さて、今回で「公差解析 基本中の基本」(1stシーズン)は終了です。
次シーズンでは、実践や応用に範囲を広げた解説をしていく予定ですので、よろしくお願いします!
――See you next season!

Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
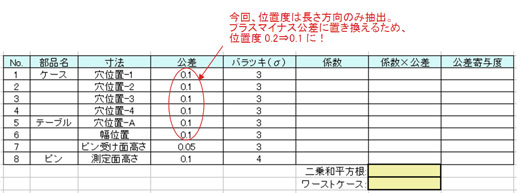 図5 公差計算シート
図5 公差計算シート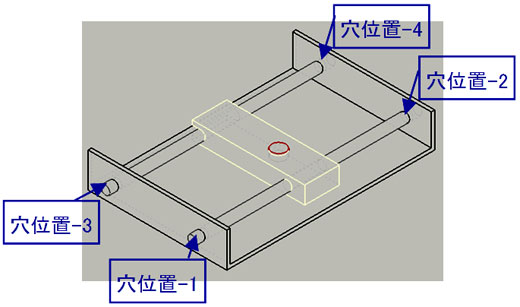 図6 ケースの穴位置の番号と位置
図6 ケースの穴位置の番号と位置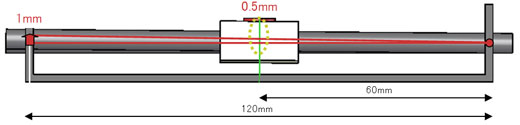 図7 ステップ1:テーブルの高さ
図7 ステップ1:テーブルの高さ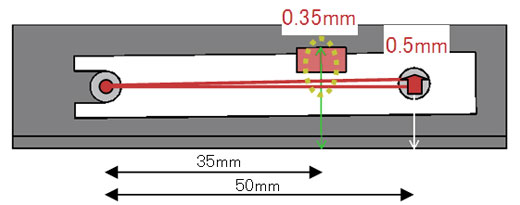 図8 ステップ2:ピンの高さ〜穴位置1と2
図8 ステップ2:ピンの高さ〜穴位置1と2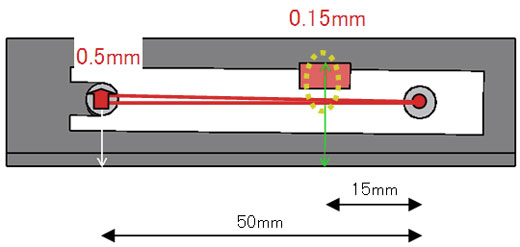 図9 ステップ2:ピンの高さ〜穴位置3と4
図9 ステップ2:ピンの高さ〜穴位置3と4 図10 穴位置、幅位置の変化
図10 穴位置、幅位置の変化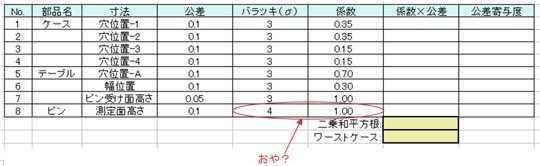 図11 公差計算シートに反映する
図11 公差計算シートに反映する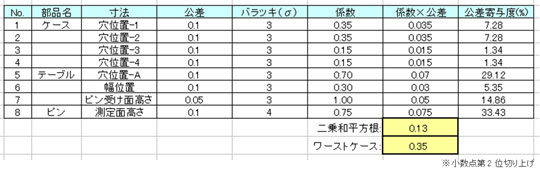 図12 できた、けど?
図12 できた、けど?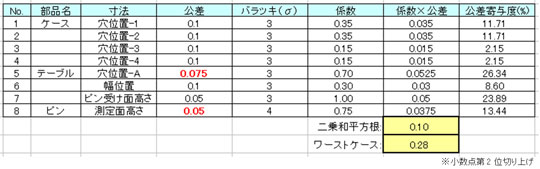 図13 ±0.1に収まっている?
図13 ±0.1に収まっている?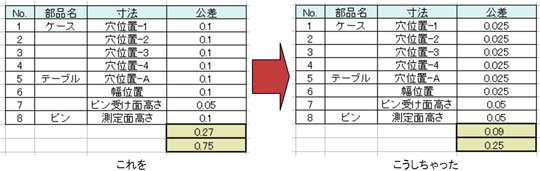 図14 オジイたちの過ちとは
図14 オジイたちの過ちとは






