有限要素法入門 〜要素剛性マトリクスの導出〜:CAEを正しく使い疲労強度計算と有機的につなげる(4)(5/7 ページ)
変数変換できたので、式26は次式となります。積分が楽になりました。
det[J]は積分で変数変換によって出てきた数で「ヤコビアン」という式38を行列式としたときの値です。
次は、変位−ひずみマトリクス[B]を求めましょう。節点変位も図6のようにξ、ηで表します。
節点変位のξ、ηの表示は次式となります。
関数N(ξ,η)は座標変換のときと同じ発想で作ることができます。N(ξ,η)とG(ξ,η)は要求される振る舞いが同様のため、同じ形にできます。N(ξ,η)とG(ξ,η)を同じ形にして要素剛性マトリクスを導きます。このようにして作られた要素を「アイソパラメトリック要素」といいます。アイソ(iso)は「同じ」という意味でしたね。
N(ξ,η)とG(ξ,η)は「形状関数」と呼ばれています。では、ひずみを求めましょう。ひずみは変位を座標xとyで偏微分したものでした。式36、式37を左側から[J]の逆行列を掛け算し、左辺と右辺を入れ替えます。次式です。
ひずみが求まったので、変位−ひずみマトリクス[B]が作れます。式39の積分は、[B]、[D]、[J]、[J]-1、|J|を先に個別に数値化して近似積分を行います。
では、20節点六面体要素ではどうでしょうか。変換前後の形状を図7に示します。
形状関数は次式となります。
形状関数は20個あります。最初の2つを書いておきます。
形状関数だけ異なる形で前述した方法で要素剛性マトリクスを作ることができます。式35や式43で表した形状関数は何かの式から導くのではなく、「ポンポンポン、チーン」という感じでぱっとひらめいて作るので、「セレンディピティ族要素」と呼ばれています。「セレンディピティ」という言葉は、『セレンディップの三人の王子たち』という童話で、セレンディップ(今のスリランカですね)の3人の王子が、その洞察力からいろいろなことを発見したことから由来しています。
2次元三角形要素と3次元四面体要素については、1次要素と2次要素の違いを説明してから触れます。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査

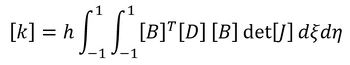 式39
式39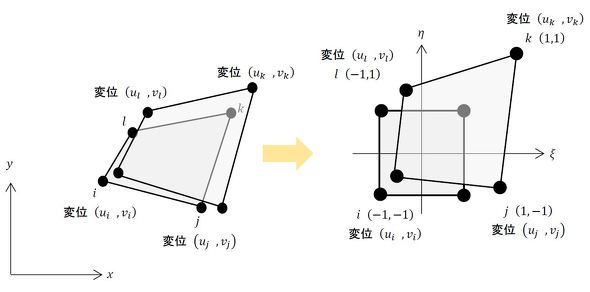
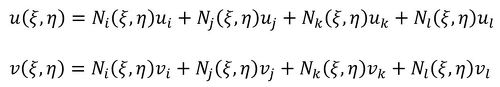 式40
式40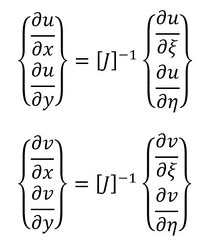 式41
式41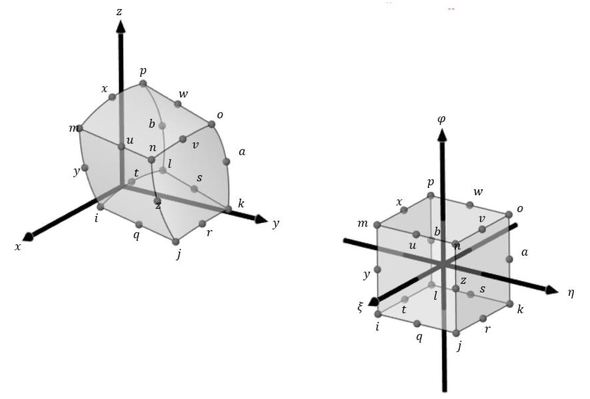
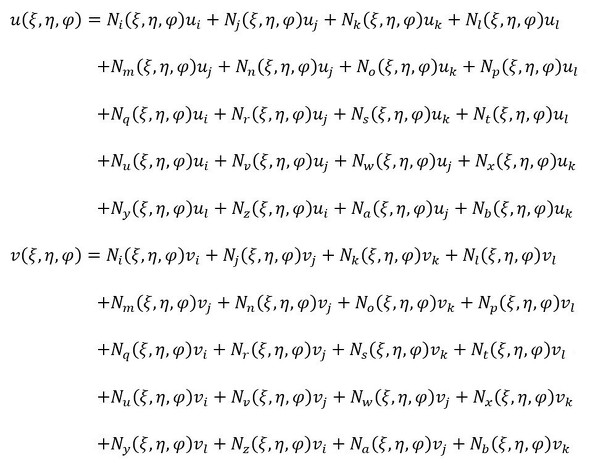 式42
式42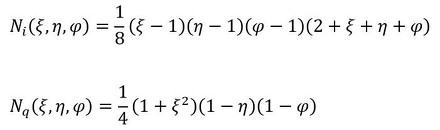 式43
式43





