有限要素法入門 〜要素剛性マトリクスの導出〜:CAEを正しく使い疲労強度計算と有機的につなげる(4)(1/7 ページ)
金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第4回は、前回に引き続き「有限要素法」について解説する。
今回お届けする連載第4回で「有限要素法」の解説はひとまず終了となります。何のために解説しているのかというと、2次要素(中間節点あり)と1次要素(中間節点なし)の計算精度の違いを説明するためです。
要素剛性マトリクスの導出:仮想仕事の原理
「仮想仕事の原理」はいろいろありますが、ここでは弾性変形問題を解くための仮想仕事の原理を使います。言葉で表現すると以下となります。
1つの質点が、これに働くいくつかの力の作用の下でつり合い状態にあるとき、この質点に微小な仮想変位を与えても、質点に働いている全ての力がこの仮想変位によってなす仕事の総和はゼロである。
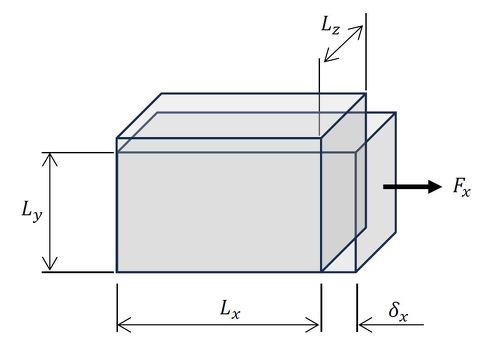
仮想仕事の原理の説明のために、弾性変形している物体に蓄えられているエネルギーを求めましょう。図1に長さLx、Ly、Lzの直方体に、x方向にFxの外力が作用し、x方向にδx伸びた状態を示します。
ヤング率の定義から、Fxとδxの関係は次式ですね。
弾性変形の最終時の荷重と変位をFx final、δx finalと表記します。伸び量がゼロからδx finalまで変化したときに外力がした仕事Wは次式となります。
式2に最終時の荷重と変位を代入して変形します。
式5を式3に代入し、応力とひずみの定義式も代入します。
式6を体積で割れば弾性体に蓄えられている単位体積当たりのエネルギーとなります。体積はLxLyLzですね。添字finalを取り除いて単位体積当たりのエネルギーは次式となります。
エネルギーは最終時の応力と変位の積の2分の1と覚えておいてください。図2に弾性変形する物体に外力Pと物体力Fが作用している状態を示します。外力Pはベクトル量で単位面積当たりの力、物体力Fは単位体積当たりの力とします。物体力Fは自重のようなものです。
変位をδu、δv、δwと表記すれば、蓄えられるエネルギーは最終時の力と変位の積の2分の1倍であることを考慮して、外力と物体力による仕事量は次式となります。
では、仮想変位の原理を式にしましょう。「全ての仕事の総和はゼロ」でした。全ての項に2分の1が付くのでこれは消去します。
式9-3Dは3次元問題の式で、式9-2Dは2次元問題の式です。以降は、式9-2Dを使います。式9-2Dの第1項は物体表面の線積分、第2項と第3項の物体の面積分です。hは三角形要素の板厚です。δu、δvは仮想変位です。「何、この式!?」と思われたでしょうが、筆者は今でもそう思っています(仮想変位の原理に対するボヤキは後述します)。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

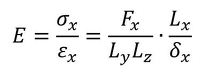 式1
式1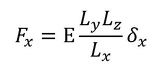 式2
式2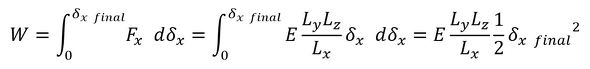 式3
式3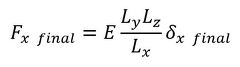 式4
式4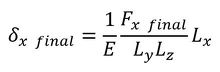 式5
式5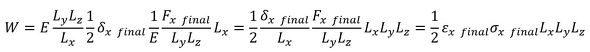
 式7
式7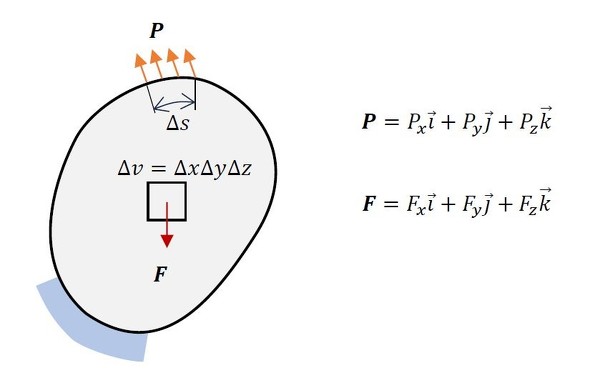
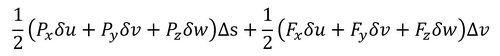 式8
式8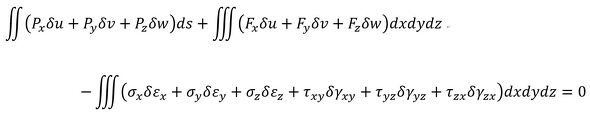
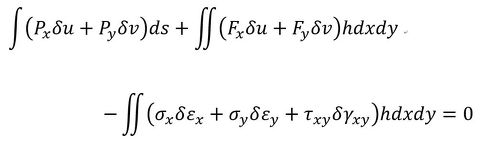 式9-2D
式9-2D





