解析ソフトは使わずに「Excel」で実験モーダル解析をやってみる:CAEと計測技術を使った振動・騒音対策(12)(2/6 ページ)
「mode1」と「mode2」の伝達関数の大きさと位相角を求める
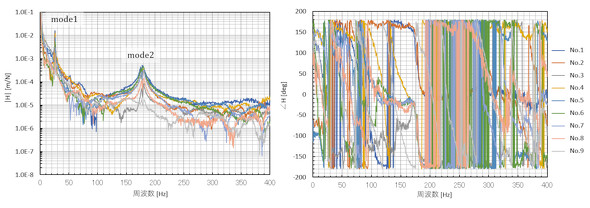
mode1とmode2の振動形状を求めましょう。これを「1次のモードシェイプ」「2次のモードシェイプ」と呼んでいます。図10に各測定点の伝達関数を示します。
振動形状を求めるには、どのような方法を使ってでも、mode1とmode2の伝達関数の大きさ(ピーク値)と位相角を抽出すればいいのです。「Excelデータになっているのだから数値を読み取ればいいじゃん!」と思われるかもしれませんが、そう簡単ではなく、カーブフィット作業が必要です。以下、カーブフィットの一例を紹介します。
測定点1の伝達関数の大きさと位相角について、23〜28[Hz]のデータを取り出したもの図11に示します。
ピークの大きさはAを選択しても、Bを選択しても大差ないようですが、位相角がAは−40[deg]、Bは−160[deg]と大違いです。「そもそも共振点の位相角は−90[deg]ではなかったのか?」とのツッコミが入りそうです。モーダル解析の位相は+90[deg]と−90[deg]だけではなく、その中間もあり得て、振動形状をアニメーション表示すると中間の位相がどのようになっているかが分かります。しかし、これでは位相角を決めることができません。
連載第8回で説明した、ばね−マス系の式を借用しましょう(式3)。
質量m、減衰係数c、ばね定数kに適当に数値を代入し、伝達関数の大きさを計算したものを図12の点線グラフ「|G|curvefit」に示します。
最初から両者が一致するわけないですね。それぞれの周波数(今回は23〜28[Hz]の9点選びました)について、測定値と|G|curvefitの差の二乗の総和をとります(式4)。
式4の値が最小となるようなm、c、kを求めるために、Excelのソルバー機能を使います。図13のような感じでしょうか。
m、c、kが求まったので、mode1の振動数は式5で求まります。
求まった後のm、c、kを使った伝達関数を図14に示します。
伝達関数の最大値は測定値よりもかなり大きくなりました。固有振動数は図11のA点とB点の中間の周波数です。
位相角は式6なのですが、アークタンジェントの引数がマイナス無限大かプラス無限大に近いので式6は使いません。図11のAとBの周波数と位相角を用いて線形補間します。−90[deg]くらいですね。
以上の操作で、mode1の測定点1の伝達関数のピーク値と位相角が求まりました。この作業を他の測定点とmode2に対して行います。合計18組の伝達関数のピーク値と位相角が得られます。ここで述べた方法は一例であって、どのような手段を使ってでも伝達関数のピーク値と位相角を求めればよいことになります。ここで求めたm、c、kは後述する「モーダルパラメーター」とは関係ない量です。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 品質はどのように作られ、どのように確認されているのか
- ソフト設計者が混乱する機械屋からの要望【安全対策編/前編】
- パナソニック コネクトがSnowflakeのAI機能を活用し、設計仕様の照合作業を9割短縮
- 協働ロボット型ペレット式3Dプリンタの基本構造「バトラー方式」で特許を取得
- 新型コロナで深刻なマスク不足を3Dプリンタで解消、イグアスが3Dマスクを開発
- 3Dプリントによる格子構造を利用した枕のクラウドファンディングを発表
- 加工不備や配線不良、バッテリー不具合、熱問題 品質課題が顕在化した1月のリコール
- 3σと不良品発生の確率を予測する「標準正規分布表」
- 3Dスキャンで伝統茶杓をデータ化、実物1点にデータ1点をひも付けて真贋証明
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化

![伝達関数:23〜28[Hz]拡大](https://image.itmedia.co.jp/mn/articles/2308/21/ay4328_shindosouon12_fig11_w490.jpg)
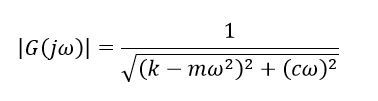 式3
式3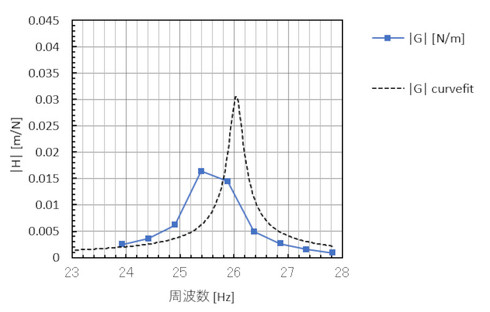
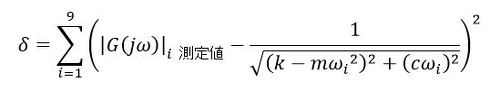 式4
式4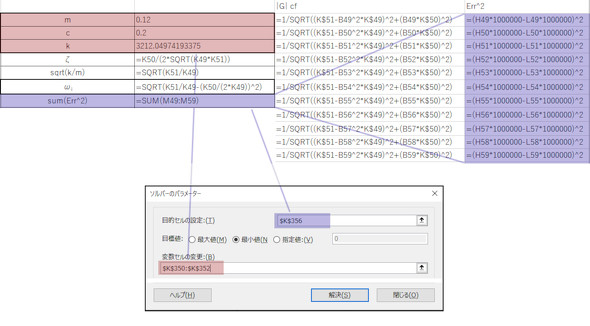
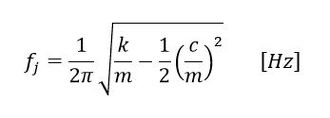 式5
式5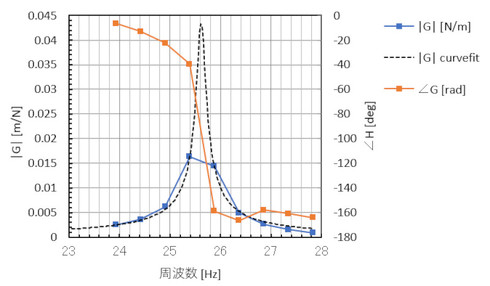
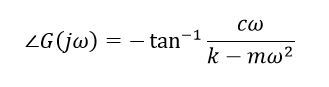 式6
式6





