解析ソフトは使わずに「Excel」で実験モーダル解析をやってみる:CAEと計測技術を使った振動・騒音対策(12)(1/6 ページ)
“解析専任者に連絡する前に設計者がやるべきこと”を主眼に置き、CAEと計測技術を用いた振動・騒音対策の考え方やその手順を解説する連載。連載第12回では「『Excel』を用いた実験モーダル解析」について取り上げる。
前回はシミュレーションによる「モーダル解析」を取り上げました。今回は実物から振動モードを求める方法、「実験モーダル解析」について解説します。
モチーフとなる構造物と測定方法
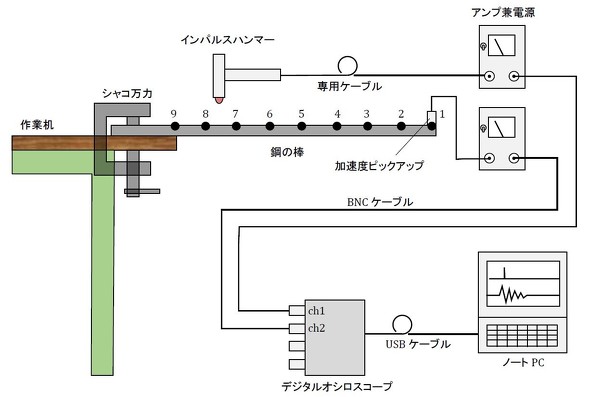
今回は分かりやすい例として、片持ちはりの振動モードを求めます。「FFTアナライザ」や「モーダル解析ソフト」を購入しなくても済む、最も安上がりな方法を紹介します。測定方法を図1に示します。
「インパルスハンマー」で鋼の棒を加振して、鋼の棒の各点の振動加速度を測定します。インパルスハンマーの加振位置は動かさずに測定点を動かしますが、測定点を動かさずにインパルスハンマーによる加振位置を動かしても同じ結果となるはずです。いずれ、インパルスハンマーによる加振ではなく、機械が実際に動いている状態のモーダル解析が必要となりますが、そのような場合は測定位置を動かすことになります。
「シャコ万力」で鋼の棒を作業机に固定し、インパルスハンマーで加振して振動加速度を「デジタルオシロスコープ」で測定します。そして、測定データはテキストファイル形式で出力して「Excel」に読み込ませます。加振側(今回はインパルスハンマー)がch1、振動側がch2なのはお約束です。インパルスハンマーがない場合は、加速度ピックアップをもう1つ用意して測定点1に付けて、その出力をch1につなげます。
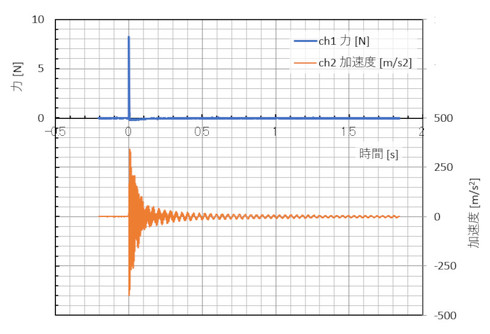
測定点1の測定データを図2に示します。力はパルス状で、振動加速度は減衰する自由振動波形となります。
伝達関数を求める
伝達関数の定義は、式1の通りです。sはラプラス変換のsです。
応答は振動変位(単位は[m])、入力は力(単位は[N])です。sにjωを代入すると伝達関数の周波数表示になります(式2)。
G(jω)の大きさ|G(jω)|と位相角∠G(jω)を求めます。連載第5回で配布したマクロプログラム付きExcelシートを図3に示します。離散フーリエ変換結果は、図3で示すように複素数で表されているので、複素数のまま計算していきます。
測定点1の振動加速度を離散フーリエ変換します。次に、加速度を変位に変換するため、離散フーリエ変換後の加速度を−ω2で割り算します。そして、変位を力で割り算します。この計算をするためのExcelシートを図4、図5に示します。A、B、H、I列は実数、C、D、E、F、G列は複素数です。今回使用したExcelの複素数計算の関数を表1に示します。関数「fft_ang()」はExcelシートを配布した際(連載第5回)に説明しました。
| COMPLEX(−(B3^2) ,0) | 複素数を生成する | |
| IMDIV(D3 ,E3) | 複素数同士の割り算 | |
| IMABS(G3) | 複素数の絶対値を求める | |
| IMREAL(G3) | 実数部を求める | |
| IMAGINARY(G3) | 虚数部を求める | |
| 表1 Excelの複素数計算の関数 | ||
図3の振幅同士を割り算し、位相同士を引き算しても同じ結果となりますが、加速度の位相と変位の位相は逆転することに注意してください。FFTアナライザを使う場合は、FFTアナライザのch1に力の信号、ch2に加速度の信号を入力すると伝達関数を直接測定できます。
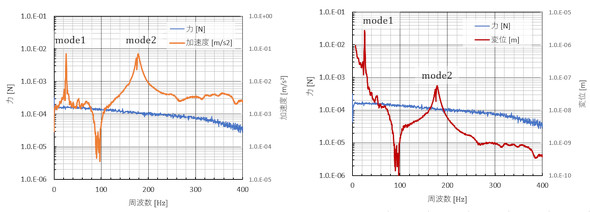
参考までに、力、加速度、変位の周波数分析結果を図6に示します。力はパルス状なので全て周波数成分を含んでいます。加速度と変位は2つの周波数でピークを持っています。1つ目を「mode1」、2つ目を「mode2」と名付けます。mode1とmode2の加速度の大きさはあまり変わりませんが、変位はmode1の方が2桁大きい値となっています。
図7に位相角を示します。ここからは意味のある情報は得られません。
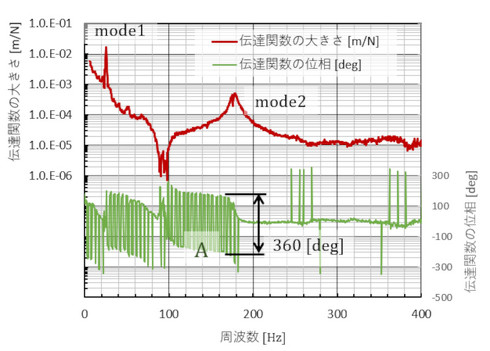
両者を引き算すると伝達関数の位相角になります。図8に伝達関数を示します。
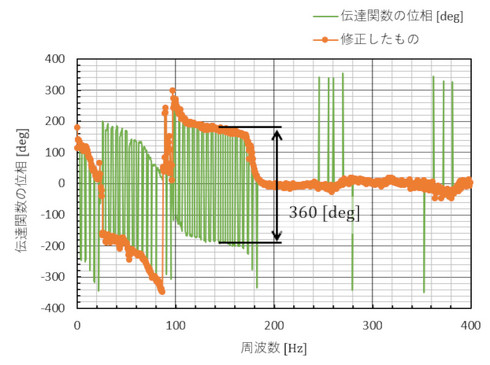
図8のA部の位相角が上下にギザギザしていて気になります。よく見るとギザギザの振幅は360[deg]です。「1周回って元の位置」という状態ですね。修正したものを図9のオレンジ色の線で示します。
mode1とmode2は共振点で、位相角は遅れる方向に変化します。90[Hz]近傍の谷は「反共振点」といって、位相角は進む方向に変化します。ここで述べる実験モーダル解析での位相角抽出には、mode1、mode2近傍の数点のデータだけを使うので、図9の修正作業は不要です。
今回は、加速度を−ω2で割り算して変位としましたが、加速度を使っても同じ振動形状が得られます。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 加工不備や配線不良、バッテリー不具合、熱問題 品質課題が顕在化した1月のリコール
- 超小型EV「mibot」開発に見る“制約を魅力へ変える”設計アプローチ
- 3Dプリンタ製の型を活用した、回せるネジ型チョコレートの取り扱いを開始
- 新型コロナで深刻なマスク不足を3Dプリンタで解消、イグアスが3Dマスクを開発
- 【レベル9】アセンブリ図面を作成せよ!
- 製造業“現場あるある”かるた<あ行:結果発表> 秀逸作品ぞろいで審査難航!?
- 品質はどのように作られ、どのように確認されているのか
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 同じ機械なのに1号機はOK、2号機はNG 設計者を悩ませる“再現しない不具合”
- 幾何公差の基準「データム」を理解しよう

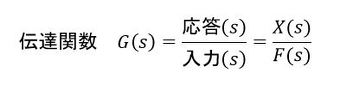 式1
式1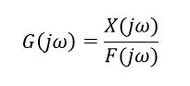 式2
式2