モデリングツールとしての「Modelica」(その1):1Dモデリングの勘所(13)(1/3 ページ)
「1Dモデリング」に関する連載。今回から3回にわたって、機械系の1Dモデリングで用いられる業界標準の表現言語「Modelica」について説明する。連載第13回では、従来の物理モデリングの方法とModelicaによる物理モデリングの方法の違いを述べた後、Modelica誕生の背景、概要、仕組み、効果、留意点について解説する。
今回から3回にわたって、機械系の1Dモデリングで用いられる業界標準の表現言語「Modelica」について説明する。
対象とする現象を定式化した後、これを計算機上に実装して解析可能とするのが「FORTRAN」などのプログラミング言語であり、さらに解析対象をモデルとして可視化するのがモデリング言語であると、ここでは定義する。
Modelicaは、プログラミング言語であるとともに、モデリング言語でもある。モデリング言語はプログラミング言語の機能も有しているので、ここでは単に“Modelicaはモデリング言語である”とする。
Modelicaでできることは多岐にわたるが、本連載ではその概要を説明するとともに、テキストベースでのモデリング(次回)、Modelica標準ライブラリ(MSL:Modelica Standard Library)を用いたモデリング(次々回)を紹介することとし、さらに高度なModelicaの使用法については、次々回の最後に関連書籍を示すので、そちらを参照されたい。
今回は、従来の物理モデリングの方法とModelicaによる物理モデリングの方法の違いを述べた後、Modelica誕生の背景、概要、仕組み、効果、留意点について説明する。
従来のモデリングとModelicaによるモデリング
例えば、FORTRANなどで、
と記述すると、これは“bの2倍をaとする”という意味で、bを入力、aを出力とすると決まっている。このような方法で記述したモデルを、入力(原因)があって、出力(結果)があることから「因果的モデル」という。
一方で、Modelicaでは、
と記述すると、これは単に“xはyの2倍である”という関係を示しているだけで、どれが入力でどれが出力とは言っていない。このような方法で記述したモデルを、因果関係がないことから「非因果的モデル」という。
従来の物理モデリング(因果モデリング)では、いったん、ユーザーが物理方程式群を手で解いた後、それらの式を記述していく方法が一般的である。
一方、非因果モデリングでは、各要素部品の間でやりとりされる物理量を定義し、各要素部品モデルの中では物理量の間で成立する関係式のみを定義しておき、それらの部品をあたかも実物のように組み合わせることで、全体システムのモデルを作成する。
従来のモデリングとModelicaによるモデリングの違いを図1に示した「一自由度系のマスダンパばねモデル」を使って説明する。これを支配する運動方程式は、
となる。
この式をラプラス変換すると、
となり、入力F(s)に対する出力X(s)の応答、すなわち伝達関数G(s)は、
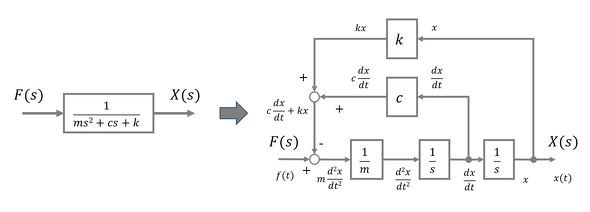
となる。この関係を、例えばブロック線図で表現すると、図2となる。これが従来の因果的モデリングによる物理モデルの一例である。
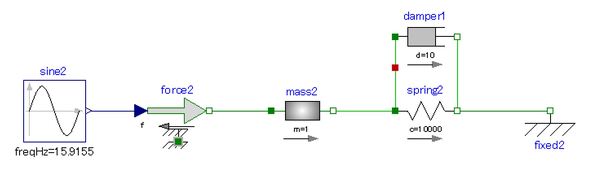
一方、非因果的モデリングであるModelicaでは、次回詳しく説明するが、関係式群をスクリプト表現でき、解析が行えるとともに、グラフィカル機能を用いて、図3に示すように、実際の機械要素(マス、ばね、ダンパ)の構成で表現することが可能だ。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
 式1
式1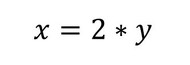 式2
式2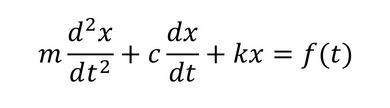 式3
式3
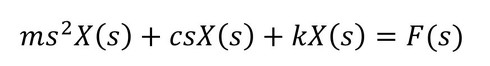 式4
式4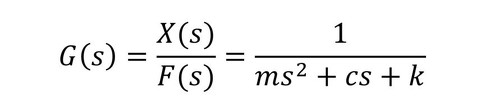 式5
式5