モデリングツールとしての「Modelica」（その1）：1Dモデリングの勘所（13）（2/3 ページ）

[大富浩一／日本機械学会 設計研究会，MONOist]

Modelica誕生の背景と特徴

　Modelicaは、1976年に、スウェーデンのLund（ルンド）大学のHilding Elmqvist氏によって考案された「Dymola（Dynamic Modeling Language）」に端を発する。これは、方程式ベースの非因果的モデリングで、モデルの再利用などを考慮した考え方が含まれていた。Elmqvist氏は情報処理の研究者で、今後より一層、多様化、複雑化する情報を見据えて、これらを統一的に扱うことのできる言語の開発を目指した。その後、多くの研究者によりモデリング言語や手法が提案され、Elmqvist氏はこれら一連の手法を取り入れ、統一言語体系とするための活動を行い、1997年に言語仕様として「Modelica 1.0」を発表した。2000年には非営利団体の「Modelica協会（Modelica Association）」（参考文献［1］）を発足し、現在に至っている。

　Modelicaによる物理モデリングは、以下のような特徴を備える。

• 要素間でやりとりされる物理量の定義と、要素内で成立する物理方程式とで、要素モデルが定義される
• 多数の要素モデルをグラフィカルエディタで結合し、システムモデルを作成できる
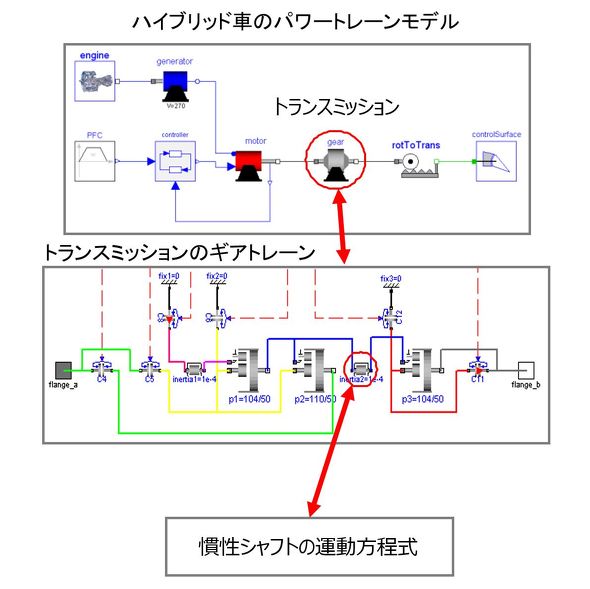
• 各モデルは階層化することが可能で、複数のサブモデルを組み合わせて、大規模なモデルも作成できる。例えば、図4に示すように、1次元回転機械系の慣性シャフトやギヤのモデルからトランスミッションのギヤトレーンモデルを作り、それにエンジン、発電機、モーターなどのモデルを組み合わせてハイブリッド車のパワートレーンモデルを作成することが可能だ

図4　Modelicaによる階層的なシステムモデルの例［クリックで拡大］

参考文献：

• ［1］Modelica協会のWebサイト（https://www.modelica.org/）

Modelicaの仕組み

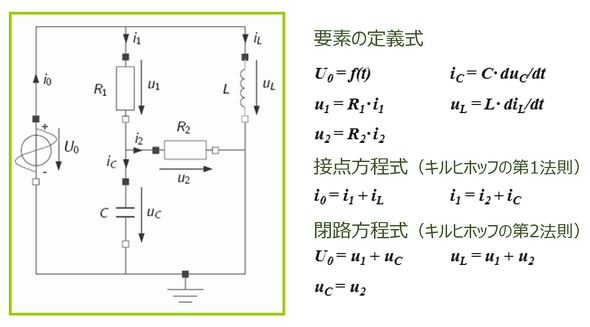
　非因果的モデリングによるモデル方程式の生成について説明する。例として、図5（参考文献［2］より引用）の電子回路のモデルを考える。

　電気系のモデルにおいては、端子間でやりとりする物理量として、電圧uと電流iが定義されている。そして、例えば、抵抗素子内では、電圧と電流の関係式（オームの法則）であるu＝R・i（Rは抵抗値）が定義されている。

　そして、回路図を描くように、グラフィカルエディタ上で部品を結合して回路モデルを作成すると、回路全体をシミュレーションするための方程式群が自動的に生成される。この際、接続した部品同士の間では、「キルヒホッフの第1法則（電流側）」（任意の節点で接続された電流の総和が0：接点方程式）と、「キルヒホッフの第2法則（電圧側）」（任意の閉回路上の電圧の総和が0：閉路方程式）に相当する定義式が追加される。接点方程式が成り立つ物理量を「フロー変数（Flow Variable）」、閉路方程式が成り立つ物理量を「ポテンシャル変数（Potential Variable）」という。

　図5の例では、右半分に示すように、10個の関係式が自動的に生成される。10個の関係式に対して、10個の未知数が存在するので解を求めることができる。ここで、これらの式は、変数間の関係のみを表し、代入式ではないことに注意してほしい。非因果的モデリングでは、代入式の右辺に表れる計算入力と、左辺に表れる計算出力を意識する必要はない。

図5　Modelicaモデルからシステム方程式自動生成の例［クリックで拡大］

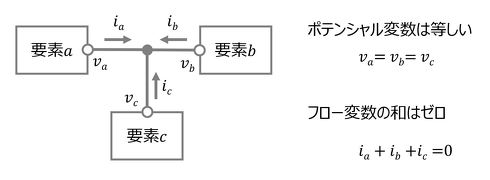
　また、Modelicaモデルの各要素間の接続関係は、図6のようになっている。ここでは、3つの要素の接続状態を示す。例えば、電気系であれば、各要素間で電圧（ポテンシャル変数）は等しく、電流（フロー変数）の和はゼロとなる。機械系では、変位（速度、加速度）がポテンシャル変数、力がフロー変数となる。

図6　Modelicaモデルの要素間の接続［クリックで拡大］

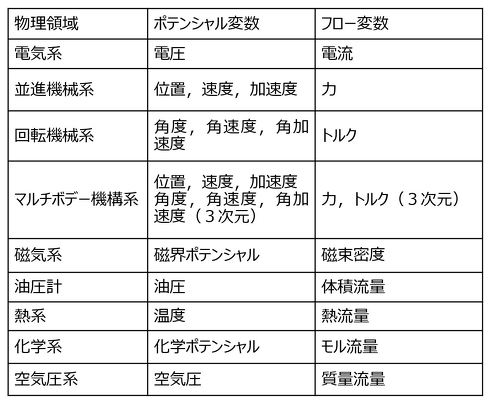
　電気系以外の他の物理系への対応としては、物理領域ごとに、表1に示すポテンシャル変数とフロー変数が定義されており、各要素モデルでは、これらの変数を用いた関係式が記述されている。これらは現象間の形式的な類似性を示しているだけで、それ以上の意味はない。一般的に、フロー変数とポテンシャル変数の積は、パワーの次元を持つ物理量となる。なお、機械系は、ポテンシャル変数として速度の次元を持つ物理量だけでなく、変位、加速度の次元を持つ物理量も使用する。また、電気モーターのように、電気エネルギーと機械エネルギーを相互に変換するコンポーネントを定義することも可能だ。このような方法により、Modelicaでは、多種多様な物理系を統一した記述法でモデリングできる。

表1　各種物理領域での変数定義［クリックで拡大］

参考文献：

• ［2］CellierFrançois. Lecture note of ‘Mathematical Modeling of Physical Systems’, Department of Computer Science, Swiss Federal Institute of Technology（ETH）Zurich.（オンライン）2012年. http://www.inf.ethz.ch/personal/fcellier/Lect/MMPS/Ppt/mmps_ppt_engl.html