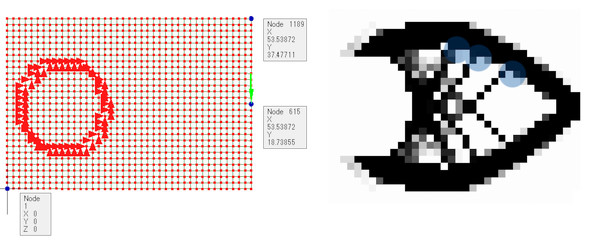
　続いて、連載第8回で、チェッカーフラグが多く出た“つり橋”を題材にします。連載第8回と少し条件を変えて、a＝0.3としました。設計空間の30［％］が実体を占めるというものです。G_targetは0.85［-］です。図17に、密度ρ_iの変化を示します。今度はつり橋のロープの部分がチェッカーフラグではなくなり、ちょっとつり橋に近づきました。

図17　橋：a＝0.3、G_target＝0.85［クリックで拡大］

　aが0.375［-］のときの、チェッカーフラグ対策あり／なしの比較を図18に示します。対策なしでは見事にチェッカーフラグができています。

図18　チェッカーフラグ対策あり／なしの比較：橋［クリックで拡大］

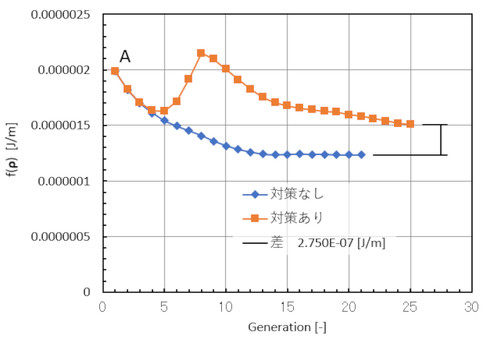
　平均コンプライアンス、つまり物体に蓄えられるエネルギーの比較を図19に示します。今度も初期の値Aよりも小さくなりました。今まで示したどの事例でも、チェッカーフラグ対策により物体に蓄えられるエネルギーは大きくなってしまいます。軽石のような“真の最適化”を追求するか、“製品にしやすい形状”にするかの分かれ道のように思います。

図19　物体に蓄えられるエネルギーの比較［クリックで拡大］

　「最適化結果は節点座標として得られるので、STL形式のデータを作って、3Dプリンタで作ればいいじゃん！」という、楽をしようとする発想はあまり賛成できません。筆者は、最適化形状を咀嚼（そしゃく）し、どういう理由で形が決まったのかを理解して、部品の設計をした方がよいと思っています。金属3Dプリンタで作った部品は、引張強度は素材の強度が出ますが、疲労強度は素材の3分の1程度ですので、後で痛い目に合うかもしれません。

Michell truss

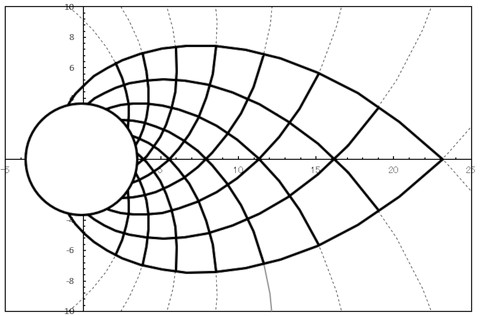
　最後に「Michell truss」（参考文献［2］）にトライします。Michell trussはコンピュータのなかった時代に発表された構造で、どのような形状にすれば強度を確保しながら材料費を減らせるかという問題の1つの解です。図20のような形をしています。極座標形式の式6で計算される曲線の集合です。それぞれの曲線が直交しているところが特徴です。

図20　Michell truss［クリックで拡大］

式6

　境界条件を図21に、最適化結果を図22に示します。参考文献［2］では、個々のトラスの太さに関する言及はないのですが、個々のトラスは同じ太さではなく、それぞれのトラスの太さにも最適解があると分かったことは収穫でした。他のトポロジー最適化による文献は、見事にMichell trussを導き出しているのですが、今回は要素数が少なかったようです。図22で青色部分が直角になった結果が得られたということでご容赦ください。

（左）図21　Michell truss：境界条件／（右）図22　最適化結果［クリックで拡大］

参考文献：

　次回から「領域最適化」に挑戦します。トポロジー最適化は設計初期段階で使用しますが、領域最適化は部品の形状が決まった後、「強度計算をしたら応力が10％足りなかった……。さて、どうしよう？」といった場面で活躍します。　（次回へ続く）

⇒ 連載バックナンバーはこちら

Profile

高橋良一（たかはしりょういち）
ＲＴデザインラボ代表

1961年生まれ。技術士（機械部門）、計算力学技術者上級アナリスト、米MIT Francis Bitter Magnet Laboratory 元研究員。

構造・熱流体系のCAE専門家と機械設計者の両面を持つエンジニア。約40年間、大手電機メーカーにて医用画像診断装置（MRI装置）の電磁振動・騒音の解析、測定、低減設計、二次電池製造ラインの静音化、液晶パネル製造装置の設計、CTスキャナー用X線発生管の設計、超音波溶接機の振動解析と疲労寿命予測、超電導磁石の電磁振動に対する疲労強度評価、メカトロニクス機器の数値シミュレーションの実用化などに従事。現在ＲＴデザインラボにて、受託CAE解析、設計者解析の導入コンサルティングを手掛けている。⇒ ＲＴデザインラボ

トポロジー最適化に挑戦する
原理原則を押さえていれば、高額なソフトウェアを用意せずとも「パラメトリック最適化」「トポロジー最適化」「領域最適化」といった“形状最適化”手法を試すことができる！　本連載ではフリーのFEM（有限要素法）ソフトウェア「LISA」と「Excel」のマクロプログラムを用いた形状最適化にチャレンジする。連載第4回では、トポロジー最適化に取り組む。
トポロジー最適化ってどうなってるの？　どうやるの？
今回は、「そもそもトポロジー最適化の背景にあるものは何か」ということと、基本的な流れについてお話します。
型抜きを考慮したトポロジー最適化とは
トポロジー最適化とかジェネレーティブデザインという言葉、引き続きトレンドではあるものの、一般的な解析同様、面白くはあります。しかし、いざ自分の環境で使おうとするとどうすればよいのか、そこがよく分からないという意見も多いのではないでしょうか？
工作機械でトポロジー最適化したらこうなった――DMG森精機
DMG森精機は「第29回日本国際工作機械見本市（JIMTOF2018）」（2018年11月1～6日、東京ビッグサイト）において、金属積層造形技術の価値を訴求するために、トポロジー最適化を駆使して実現した工作機械を参考出典した。
トポロジー最適化（位相最適化）
メカ設計者のための用語辞典。今回は「トポロジー最適化（位相最適化）」について解説する。
マンボウに学ぶBWB型旅客機の構造設計、CFRP 3Dプリンタも実現を後押し
JAXA 航空技術部門構造・複合材技術研究ユニットでは、バイオミメティクスを取り入れたトポロジー最適化を、現在、新たな旅客機の形として注目されている「Blended Wing Body（BWB：翼胴一体）」機の構造設計に適用することで、旅客機のさらなる性能向上、技術革新を図ろうとしている。同ユニットの主任研究開発員である星光氏と有薗仁氏に話を聞いた。