実践！ 密度法によるトポロジー最適化に挑戦してみよう：フリーFEMソフトとExcelマクロで形状最適化（7）（4/6 ページ）
片持ちはりのトポロジー最適化
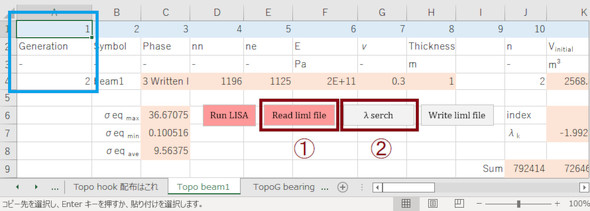
Excelに戻ります。図17のA4セルに注目してください。世代が1世代進んでいます。第2世代以降はA4セルをプログラムが更新します。［Read liml file］ボタンを押して、続けて［λ search］ボタンも押下してください。
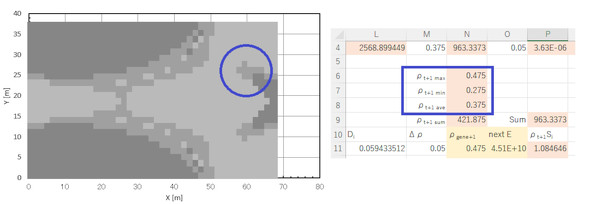
ρiの分布を図18に示します。何やら骨が生えてきました。N6〜8セルに注目します。ρiの最大値が0.475［-］、最小値が0.275［-］になりました。ρiの最大値／最小値が「1」と「0」になるまでを目安として、この作業を繰り返します。ρiの平均値が0.375［-］を維持していることを確認しておきます。
次に［Write liml file］ボタンを押して、次の世代のLISAファイルを生成します。このような作業を16回くらい繰り返します。
最適化結果の評価
図19に、ρi分布の変化を示します。黒色の部分のρiは「1」で、白色の部分のρiは「0」です。ρi＝1の領域が最適化形状を示しています。ρi＝0の領域は肉抜き部です。少しグレー（灰色）のところがありますが、これ以上進めると大切な小骨が消滅してしまうので、人間の判断で終了します。最終形状よりも、それに至るまでの過程を見ている方が楽しいですね。
では、参考文献［1］の結果と比較してみましょう。参考文献［1］は「均質化法」なのでやり方が異なるのですが、“ほぼ同じ最適化形状”となっています。参考文献［1］で示されている通りパラメータを変えることによって、最適化形状は1つではなくいろいろなパータンが存在します。
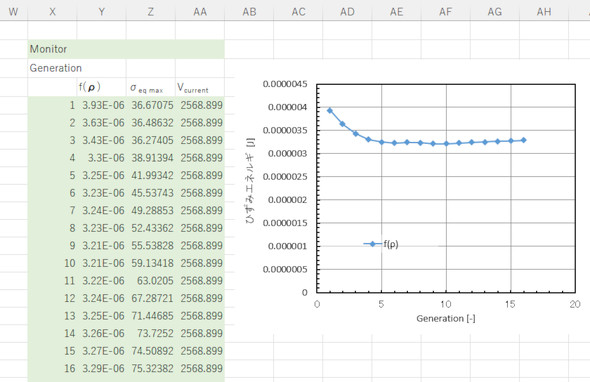
図20に、f（ρ1、ρ2、ρ3……ρne）の変化を示します。この量は物体に蓄えられる仕事量（ひずみエネルギー）ですが、平均コンプライアンスでもあり、はりの剛性の逆数でもあります。物体に蓄えられる仕事量が順調に小さくなっています。つまり、剛性最大化ができています。第5世代くらいで底を打っていますが、最適解というのはグレー領域がある状態だといえます。肉抜きではなく、物体の一部を軽石のようにするのが最適解だと解釈できます。
以上がトポロジー最適化の手順です。次回はいろいろな問題について、トポロジー最適化手法を使って形状を創造していきます。お楽しみに！ （次回へ続く）
※次ページ以降は、今回の内容に関連する「付録（プログラムリスト）」となります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
ITmediaはアイティメディア株式会社の登録商標です。