パラメトリック最適化に挑戦する:フリーFEMソフトとExcelマクロで形状最適化(2)(4/4 ページ)
はりの体積
その前にはりの体積を求めます。体積は式32で表されます。
ここで式33に示すような関数g(n,a)を導入します。
体積がVoと等しくなるという条件は、g(n,a)=0が成立するということになります。
g(n,a)=0が成立し、コンプライアンスが最小になるようなはりの形状を求めるという問題は、数学では次式で表現します。
見慣れない記号ℜが出てきましたね。ℜは「実数全体」という意味で、nとaは“実数の範囲で見つけてください”ということになります。そりゃそうですね。nとaが複素数でしか解がないとなると都合が悪いですね。f(n,a)を目的関数、g(n,a)を制約関数といいます。
それと、「体積は小さい方がいい!」といって、少し欲張って式35を式36に変えるようなことはしません。こうすると「Karush-Kuhn-Tucker条件(KKT条件)」というものを導入しなければならず話が難しくなります。本連載では、制約関数には等式を使うことにします。
次回は、「ラグランジュの未定乗数法」を使って、コンプライアンスが最小となるようなnとaを求めます。どのような結果となるでしょうか。Wikipediaの説明(参考文献[2])で十分ですので、少し予習していただければ幸いです。 (次回へ続く)
Profile
高橋 良一(たかはし りょういち)
RTデザインラボ 代表
1961年生まれ。技術士(機械部門)、計算力学技術者 上級アナリスト、米MIT Francis Bitter Magnet Laboratory 元研究員。
構造・熱流体系のCAE専門家と機械設計者の両面を持つエンジニア。約40年間、大手電機メーカーにて医用画像診断装置(MRI装置)の電磁振動・騒音の解析、測定、低減設計、二次電池製造ラインの静音化、液晶パネル製造装置の設計、CTスキャナー用X線発生管の設計、超音波溶接機の振動解析と疲労寿命予測、超電導磁石の電磁振動に対する疲労強度評価、メカトロニクス機器の数値シミュレーションの実用化などに従事。現在RTデザインラボにて、受託CAE解析、設計者解析の導入コンサルティングを手掛けている。⇒ RTデザインラボ
関連記事
 見せてもらおうか、FreeCADのFEMワークベンチの実力とやらを!
見せてもらおうか、FreeCADのFEMワークベンチの実力とやらを!
オープンソースの3D CAD「FreeCAD」をご存じだろうか。無償でありながら、3Dモデリング、メッシュデザイン、製図(ドラフト)、有限要素法解析(FEM)、レイトレーシング、ロボティクス機能など、標準機能がとにかく充実している。本連載では「FreeCAD 0.18」を用いて各機能の実際の操作や使用感を紹介していく。連載第6回では、FreeCADの標準ワークベンチである「FEM」の使用感をレビューする。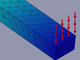 無償3D CAD「FreeCAD」でFEM解析に挑戦!
無償3D CAD「FreeCAD」でFEM解析に挑戦!
無償のCADソフト「FreeCAD」にはFEM解析機能が標準で搭載されていて、モデリングした部品の応力や変形を簡単にシミュレートできる。今回は片持ち梁(かたもちばり)の解析でFEM機能を試してみる。 FEMの知識総まとめ〜あなたの解析は設計後?〜
FEMの知識総まとめ〜あなたの解析は設計後?〜
設計が終わってから解析している人、本当にそれで大丈夫? 手戻り発生を極力防ぐ解析のタイミングとは 無償の流体解析ソフト「Flowsquare」をインストールしよう
無償の流体解析ソフト「Flowsquare」をインストールしよう
無償で使える流体解析ソフト「Flowsquare」を使ってみよう! 今回はソフトのインストール&起動編。 無償の工学計算ソフト「FreeMat」をインストールしよう
無償の工学計算ソフト「FreeMat」をインストールしよう
無償の工学計算ソフトでも、かなり高度な計算ができる! 今回はインストール編。工学計算の初心者もぜひチャレンジしよう。 その設計、そのボルトと本数で大丈夫?
その設計、そのボルトと本数で大丈夫?
部品の固定(締結)のために使用する“ボルトの設計”をテーマに、設計者向けCAE環境を用いて、必要とされる適切なボルトの呼び径と本数を決める方法を解説する。また、連載の中で、ボルト締結の基礎である締め付けトルクと軸力の関係や、締め付けトルクの決定方法などについても取り上げる。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現

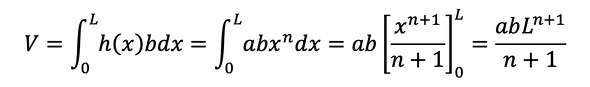 式32
式32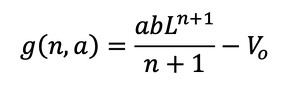 式33
式33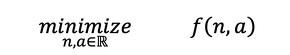 式34
式34






