パラメトリック最適化に挑戦する:フリーFEMソフトとExcelマクロで形状最適化(2)(2/4 ページ)
関数の極大値と極小値
「何をいまさら」なのですが、関数の極大値と極小値を求めましょう。例えば、下に凸の関数(y=f(x)=x2など)の極小値は、関数を微分することで求まります。極小値になる条件は以下でしたね。
y=xnの場合は、式10となります。
少し余談になりますが、式10は1684年にライプニッツによって証明抜きで発表されましたが、次の積分の式はその20年ほど前にヨーロッパの数学者の間で知られていました(参考文献[1])。積分の方が早かったのです。
参考文献:
- [1]志賀浩二/数学の流れ30講(中)/朝倉書店(2019)
式10と式11は、これから多用していきます。
以下に、凸の関数の極小値の例を示します(図4)。
では、変数がたくさんある場合を考えましょう。先ほど変数を座標xとしましたが、座標だとy、zと変数が3つで終わりなので、x、y、zの代わりに、ρ1、ρ2、ρ3、ρ4、ρ5……ρmとしましょう。これらの変数は、図1のC1、C2、C3などに相当した設計変数で、設計変数はm個あります。図2の片持ちはりの場合、m=2、ρ1=n、ρ2=aとなります。
ある関数f(ρ1,ρ2,ρ3……)があるとし、その極小値ないしは極大値となり得るρ1、ρ2、ρ3……はどうやって求めるのでしょうか。次に示す連立方程式を解くことによって求めます。連立方程式は設計変数の数だけ(m個)あります。
偏微分の記号∂が出てきました。式12-1の場合、ρ1を変数としてρ1だけで微分し、ρ2以降を定数として扱います。つまり、定数の微分なのでゼロとなります。極小値は図5のようになります。最適化問題でよく見かける図ですね。
剛性最大化、コンプライアンス最小化
形状最適化の文献には「剛性最大化」という表現ではなく、「平均コンプライアンス最小化」という表現が使われています。コンプライアンスは、ばね定数の逆数なので、剛性最大化問題は平均コンプライアンス最小化問題となります。コンプライアンスfは式13で定義されます。
力×変位(移動量)になるので、仕事量[J]と同じ単位となります。ばね定数k[N/m]を導入しましょう。変位uは、荷重Wをばね定数kで割ったものなので、式13は次式となります。
分母にばね定数kが出てきたので、コンプライアンスはばね定数の逆数となります。では、W=kuを代入しましょう。
ばねに蓄えられるエネルギーEは式16だったので、コンプライアンスはばねに蓄えられるエネルギーの2倍ですね。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- シーリングファンで合計2万台リコール ただし、安全設計により落下事故はゼロ
- デンソーが搬送ラインにラティス構造柔軟指を導入 多様な形状のワークに対応
- 筆者の経験したODMに関するエピソード【前編】 〜部品表の重要性〜
- 誰でも「マジンガーZ」の操縦者に! 全身3Dスキャンとフルカラー3Dプリンタで
- 量子コンピュータ上の非線形方程式の計算を指数関数的に加速させる手法を開発
- 金属3Dプリンタと未利用木材を組み合わせた建築モジュール
- IOWN APNを用いた「世界初」の3D CAD遠隔共同作業の実証に成功
- Japan Mobility Show 2025 レポート【メカ設計編】
- 3σと不良品発生の確率を予測する「標準正規分布表」
- 知っておきたいJISから見た機械材料 〜鋼の種類と違い〜

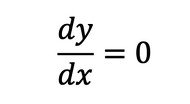 式9
式9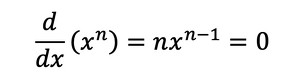 式10
式10 式11
式11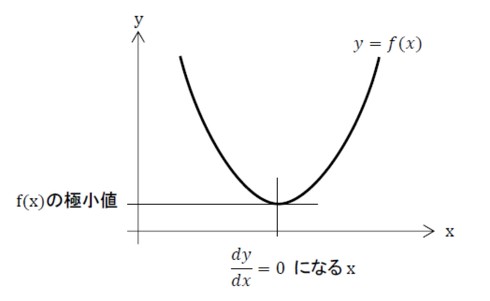
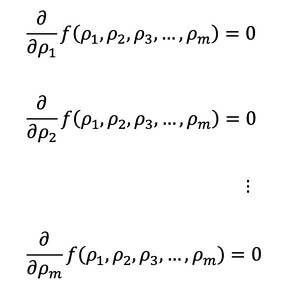 上から式12-1/式12-2/式12-m
上から式12-1/式12-2/式12-m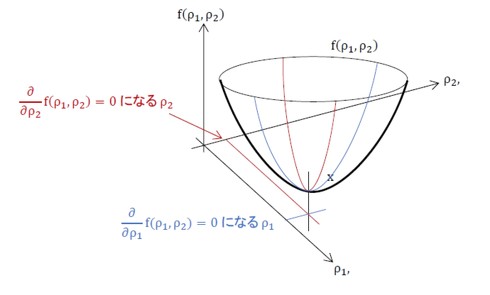
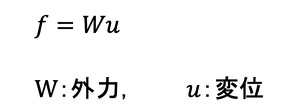 式13
式13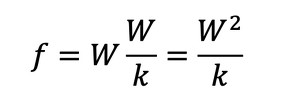 式14
式14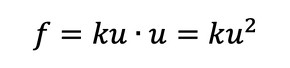 式15
式15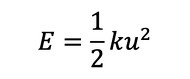 式16
式16





