パラメトリック最適化に挑戦する:フリーFEMソフトとExcelマクロで形状最適化(2)(1/4 ページ)
原理原則を押さえていれば、高額なソフトウェアを用意せずとも「パラメトリック最適化」「トポロジー最適化」「領域最適化」といった“形状最適化”手法を試すことができる! 本連載ではフリーのFEM(有限要素法)ソフトウェア「LISA」と「Excel」のマクロプログラムを用いた形状最適化にチャレンジする。連載第2回では片持ちはりをモチーフに、パラメトリック最適化について解説を始める。
本連載で取り上げる形状最適化は、以下の3つとなります。
- パラメトリック最適化
- トポロジー最適化
- 領域最適化
「パラメトリック最適化」については手計算で、「トポロジー最適化」と「領域最適化」に関しては、フリーのFEM(有限要素法)ソフトウェアとマクロプログラム付き「Excel」を用いて解説していきます。
パラメトリック最適化について
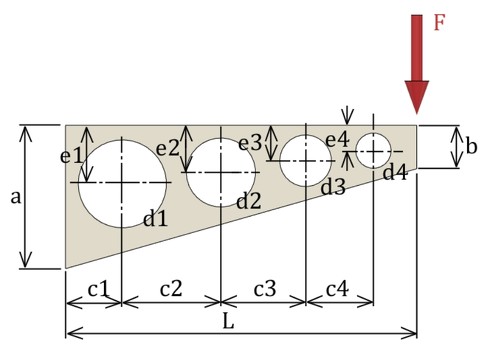
まず、パラメトリック最適化から説明します。例えば、図1のような部品の設計を考えましょう。形状がいくつかのパラメータで定義されていて、3D CADによる形状定義は「パラメータ設計」といってよいでしょう。図1の場合、寸法値が設計パラメータです。ここでは、荷重Fに対する変形量が最小となるようなパラメータを求めることを目標とします。連載第1回でも述べましたが、変形量を最小化する目標を達成した形状の応力分布は、応力の高いところと応力の低いところが均一化されていて、強度面でも最適化されている場合が多いです。
図1ではパラメータが多過ぎるので、今回は図2に示すような穴のない片持ちはりをモチーフにします。高さhが座標xの関数で、h=axnであるとします。荷重に対する変位が最小となる、つまり剛性が最大となるパラメータnとaはいくらになるでしょうか。
片持ちはりの応力
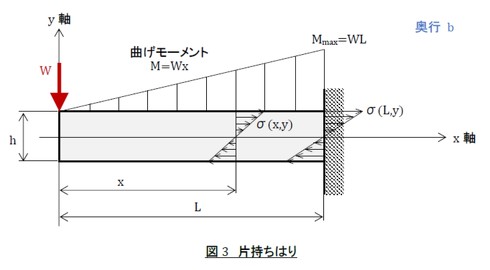
「何をいまさら」と思われるでしょうが、片持ちはりの応力をおさらいしておきましょう。曲げモーメントはM(x)=Wx、最大曲げモーメントははりの根元で発生し、Mmax=WLですね。
xの位置の曲げ応力はxとyの関数となり、式2で表されます。
上下端(y=±h/2)の応力は式3となります。
断面二次モーメントIは式4でした。
今、はりの高さhが座標xによって、h(x)=axnのように変化するとしましょう。断面二次モーメントは式5となります。
式5と式1を式3に代入し、プラスの応力だけを考えましょう。
xのどの位置でもσ(x)が変化しないようなはりを考えます。つまり、σ(x)がxの関数でなくなるようなはりです。式6において、1−2nがゼロになればσ(x)がxの関数ではなくなりますね(式7)。
式7を式1に代入します。
はりの高さh(x)がxのルートに比例するようにすれば、xのどの位置でも曲げ応力が一定となります。平等強さのはりですね。しかし、これから求めるのは、荷重Wに対する変位が最小になるようなはりです。どうなるのでしょうか。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現

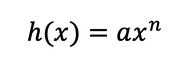 式1
式1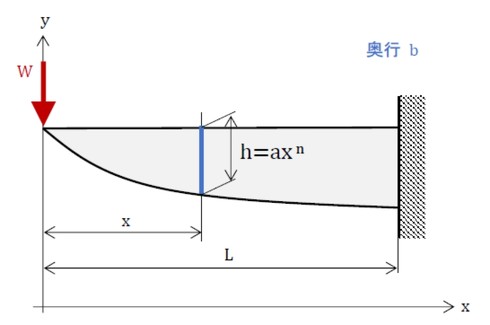
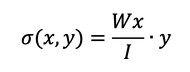 式2
式2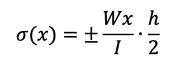 式3
式3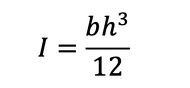 式4
式4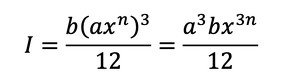 式5
式5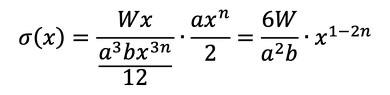 式6
式6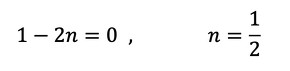 式7
式7





