パラメトリック最適化に挑戦する:フリーFEMソフトとExcelマクロで形状最適化(2)(3/4 ページ)
コンプライアンスを最小化するはりの形状
先ほど「荷重Wに対する変位が最小になるようなはり形状を求めましょう」と述べましたが、剛性最大化問題はコンプライアンス最小化問題のことになるので、表現を変えて「コンプライアンスが最小」となるはりの形状を求めましょう。はりの形状は、例えばスプライン曲線で表現してもいいのですが、今回ははりの高さh(x)が式1で限定されたはりの形状を求めましょう。
はりのたわみ曲線を求める基礎方程式は式17です。yがたわみ量[m]、Eはヤング率E[Pa]です。
曲げモーメントMと断面二次モーメントIが座標xの関数となります(式18)。
式18を式17に代入します。
式19をxで積分します。積分定数をC1としておきます。
C1を求めます。x=Lではりの傾きはゼロなので式21が成立します。
式21を式20に代入しておきましょう。
次はたわみ量です。式22をxで積分します。
C2を求めます。x=Lで、はりのたわみはゼロなので次式が成立します。
たわみは式26となります。
x=0のときのたわみを変位uとして、コンプライアンスを求めます。
たわみは下方向なのでマイナス値となりました。プラスに変えて、コンプライアンスは式28となります。
今考えているのはコンプライアンスの最小化で、設計変数がnとaです。式12でのf(ρ1,ρ2,ρ3……ρm)が式28に相当し、これを目的関数と呼びます。目的関数を設計変数の関数とすると、式29で表すことができます。
では、式12に従って式24をnとaで偏微分し、イコールゼロとしましょう。
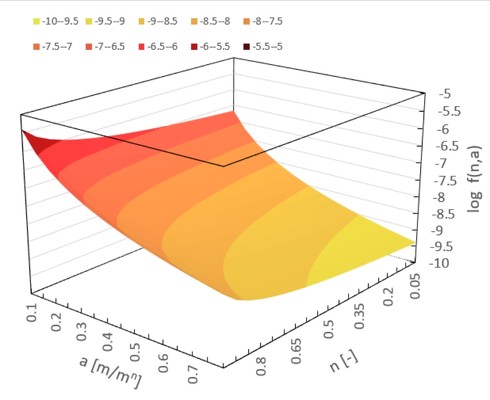
この連立方程式を解くのは難しそうです。変数をnとaとして目的関数fを図6のようなグラフで表現しました。
むむ……。図5に示したような極小値がありません。nが0.05[-]より小さく、aが0.8[m/mn]より大きいところに極小値があるというのでしょうか。nがマイナス値であるとは考えられないため、n=0[-]が解で、hはxによらず一定値ということなのでしょうか。違うような気がします。図6を見ると「aは大きければ大きいほど良い」と読み取れます。そりゃそうですね。はりの高さhが大きいほど剛性は高くなります。
制約条件を入れる必要があります。aを大きくするとはりの体積が増えます。はりの体積が一定値Voという条件を入れましょう。体積がVoという制約の中で、コンプライアンスが最小(剛性が最大)となるようなnとaを求めましょう。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- ソフト設計者が混乱する機械屋からの要望【安全対策編/前編】
- 品質はどのように作られ、どのように確認されているのか
- 協働ロボット型ペレット式3Dプリンタの基本構造「バトラー方式」で特許を取得
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 超小型EV「mibot」開発に見る“制約を魅力へ変える”設計アプローチ
- 3Dプリントによる格子構造を利用した枕のクラウドファンディングを発表
- パナソニック コネクトがSnowflakeのAI機能を活用し、設計仕様の照合作業を9割短縮
- 新型コロナで深刻なマスク不足を3Dプリンタで解消、イグアスが3Dマスクを開発
- 3Dスキャンで伝統茶杓をデータ化、実物1点にデータ1点をひも付けて真贋証明
よく読まれている編集記者コラム

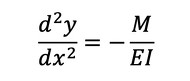 式17
式17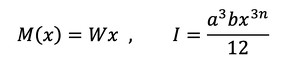 式18
式18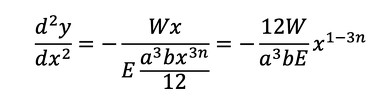 式19
式19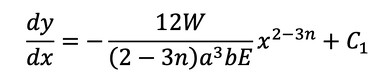 式20
式20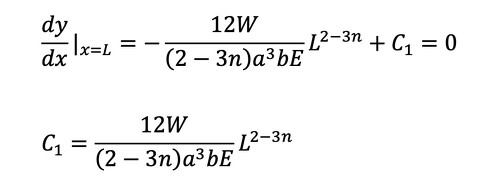 式21
式21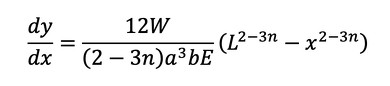 式22
式22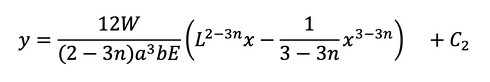 式23
式23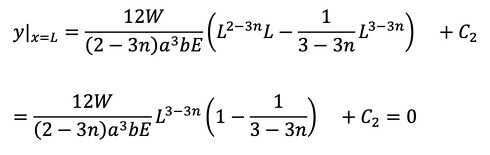 式24
式24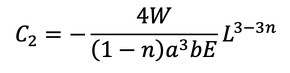 式25
式25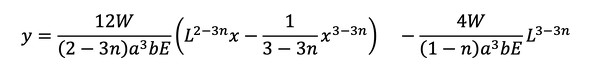 式26
式26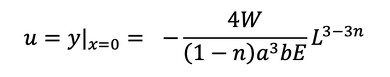 式27
式27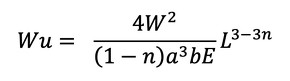 式28
式28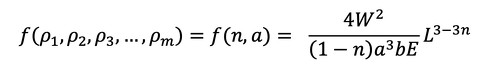 式29
式29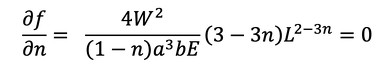 式30
式30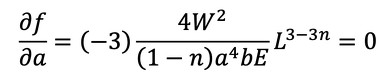 式31
式31