ボルトの緩み対策:設計者向けCAEを使ったボルト締結部の設計(9)(4/5 ページ)
ダッシュポットはなぜピストンのような記号なのか
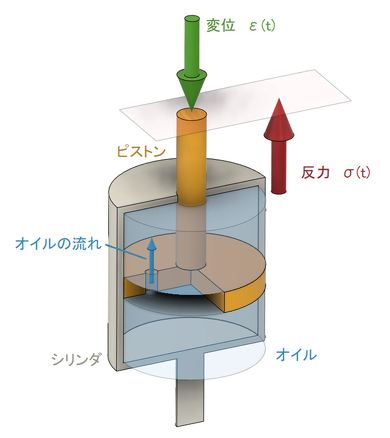
図9に示しましたが、ダッシュポットはなぜピストンのような記号なのでしょうか。少し脱線しますが、ダッシュポットを図10に示します。
シリンダの中にオイルが満たされていて、ピストンがシリンダの部屋を2つに分けています。そして、ピストンには小さな穴が開いています。ピストンに下向き荷重を加えると、オイルが下の部屋から上の部屋へと小さな穴を通って移動します。オイルが小さな穴を通るときに流体摩擦が生じて、下の部屋の圧力と上の部屋の圧力に差が生じます。流れが層流の場合、この圧力差はハーゲン・ポアゾイユの式によると、ピストンの移動速度に比例します。そして、この圧力差によってピストンに上向きの力が発生します。ピストンの移動に対する抵抗力ですね。このような仕組みでダッシュポットは移動量の速度、つまり移動量の時間微分に比例した抵抗力を発生します。ピストンとシリンダを模してこのような記号になっています。
Maxwellモデルに戻りましょう。図11です。ばねEの縮み量をε1(t)、ダッシュポットcの縮み量をε2(t)とします。ボルトの初期締結力をσ0とし、ボルト締結は瞬時に行われるとすると、被締結体のダッシュポットは瞬時に変形できないのでt=0[s]におけるε2(t)の初期値はゼロとなります。よって、変形はばねだけで発生することになり、ε1(t)の初期値はσ0/Eとなります。
ボルト締結という行為は、被締結体が瞬時に縮められて、その縮められた量が時間の経過に関係なく一定値を保つということです。つまり、変位の和は常に一定で、次式で表されます。一方、被締結体によるボルトへの反力σ(t)は時々刻々低下します。
式1をε2(t)に書き換えます(式6)。
Eとcは直列つなぎなので、σ(t)とε1(t)には次の関係があります(式7)。
式5、式6、式7は、変数分離ができて被締結体の反力は次式で表されます(式8)。
う〜ん。都合が悪いですね。式8によると、時間の経過とともにσ(t)がゼロに近づきます。どんなに増し締めしても、いずれボルトの軸力はゼロになってしまいます。しかし、参考文献[8]のガスケットの例などで代表されるように、増し締めすれば、長い間軸力が保持されることは経験的に分かっています。モデルを変える必要があります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現


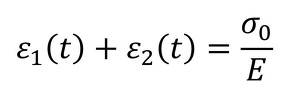 式5
式5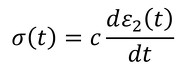 式6
式6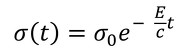 式8
式8





