流体解析のメッシュ、どこまで細かくしたらよいのか:CAE豆知識
メッシュサイズは解の品質を左右します。でも細かくなれば、計算時間もどんどん増えます。
本記事は、CADを快適な環境で使ってもらうソリューション専門街「CADJapan.com」から転載しています。
本格計算に入る前にトライしたい、メッシュの感度解析
流体計算の結果はどれくらい信頼できるのか? これまで実測で済ませてきた現場に流体ソフトを導入するとき、必ず議論となるテーマではないでしょうか。解析解との比較や実測値と比較して流体ソフトを検証することは確認(verification)と検証(validation)と呼ばれ、ソフトの品質保証の観点から重視されるようになってきています。
メッシュのサイズは解の品質を左右する重要な要因となっています。問いに対する1つの回答は「メッシュをそれ以上細かくしても得られる解が変化しなくなるサイズ」です。計算量はメッシュ数に比例します。3次元定常計算の場合、メッシュサイズを半分にすると計算量は2の3乗に比例して増加することになります。
メッシュを細かくするにつれ計算時間が急激に増大するため、現実的な時間で結果を得るためにはどこかで妥協する必要があります。場合によっては現実的な時間で予測計算を終了することができないと判断せざるを得ない場合もあるかもしれません。右の図はこの関係を模式的に表したものです。
感度解析の例(バックスステップ流れ)
粘性流れの検証問題として採用されることの多いバックステップ流れを例にメッシュの感度解析を行ってみます。メッシュ数によって再付着点(図の矢印の位置)の予測がメッシュサイズによってどのように変化するかを調べます。
ステップの高さをHとしたときダクトの高さは2H、計算領域の長さは11Hとします。Re=200とします。Hの分割数を4,8,16,32と変えて計算してみます。再付着点の位置は壁面から第1メッシュのセル中心で長手方向の流速成分の符号がマイナスからプラスに変化する位置の座標として算出します。
このとき再付着点の計算値とメッシュ数(Hの分割数)の関係をまとめると下のグラフのようになりました。この結果から16分割以上にメッシュ数を増やしても計算精度は向上しないことが分かります。メッシュ数の増加につれ、計算時間は急激に増加しますので16分割以上の計算を実施してもコストに見あう精度向上は望めません。
このような検討をおこなうためにはメッシュ数を変えた計算を最低3ケース実施することが必要です。使用している流体計算法の空間精度(1次、2次など)が分かっている場合は、メッシュ数によって結果が変動している場合でも、収束値を外挿して予測する手法もあります。
いざ計算を始めたものの、いつになったら計算が終了するのか途方にくれたことはないでしょうか。いつでもこのような感度解析が可能かどうかは分かりませんが、本番の計算に入る前に試みることをおすすめします。
関連記事
 空気が流れる空間をメッシュで細かく刻む
空気が流れる空間をメッシュで細かく刻む
解析の頭脳「ソルバ」をうまく動かすには、適切なメッシュ作成が肝心だ。今回はメッシュの基礎から解説する 超重要! メッシュサイズと8つの質問
超重要! メッシュサイズと8つの質問
解析精度を高めるため設計者自身でコントロールできる唯一のパラメータは、メッシュサイズだ。 ソリッド四面体1次要素は、デンジャラス!?
ソリッド四面体1次要素は、デンジャラス!?
ソリッド四面体要素を使うときの、大事な約束がある。それを守らないと、危ない結果が待っている!?
関連リンク
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 義手とロボットの手を共通化するPSYONICのバイオニックハンド「Ability Hand」
- 約3.5kgの力で打ち抜ける手動式卓上パンチプレス
- 高精度3Dスキャナー3機種を発売、自動検査や医療分野を支援
- 同じ機械なのに1号機はOK、2号機はNG 設計者を悩ませる“再現しない不具合”
- 新型コロナで深刻なマスク不足を3Dプリンタで解消、イグアスが3Dマスクを開発
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 幾何公差の基準「データム」を理解しよう
- 令和版の健康サンダル? 否、感覚を増幅する「Nike Mind」が気になる件
- 3σと不良品発生の確率を予測する「標準正規分布表」
- 強度設計の出発点 “計算”より先に考えるべきこととは?

 計算時間とメッシュ数の関係
計算時間とメッシュ数の関係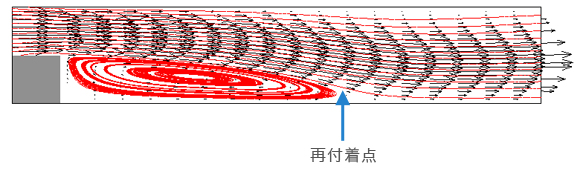 感度解析の例(バックスステップ流れ)
感度解析の例(バックスステップ流れ)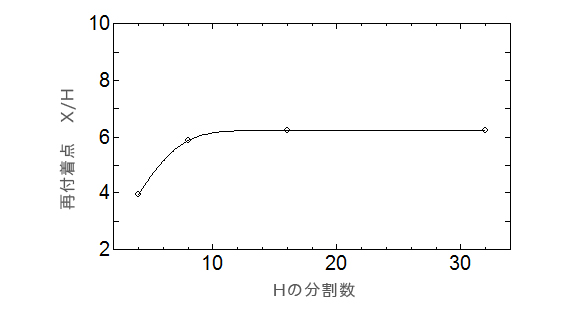 再付着点の計算値とメッシュ数(Hの分割数)の関係
再付着点の計算値とメッシュ数(Hの分割数)の関係





