「形体をコントロールする方法を覚えよう」の巻:ママさん設計者がやさしく教える「図面の読み描き超入門」(3)(3/5 ページ)
幾何公差の種類
表1の通り、幾何公差には幾つもの種類があります。図面の中に幾何公差を見つけたらこの表と照らし合わせて、図面に込められた設計者の意図(思い)を理解しましょう。
そして、これが関連形体での幾何公差の表し方です(図3)。データムが必要でない単独形体での幾何公差では、記号と公差値までを記入します。
幾何公差はかわいそうな存在?
寸法公差と幾何公差について理解できましたでしょうか。ただ、ここで勘違いしてはいけないのが、寸法公差と幾何公差で“がんじがらめ”な図面でも、加工者の腕が良ければ何とかモノにしてくれるだろうという思い込みです。加工者は神様ではありませんので、加工方法によっては設計者の意図を100%完全に実現できないこともあり得ます。図面上で描かれた部品は、あくまでも「バーチャルリアリティ」でしかないのです。
ですから、設計者は公差検討の前に、その箇所をどのように加工して、どのように測定するのかを考える必要があります。そのためには、やはりある程度の加工経験は必要なのかなと思います。
実際、幾何公差が入った図面を渡すと、重い表情で眺める加工者もいます。たとえ寸法公差が「長さ寸法および角度寸法に対する普通公差(JIS B 0405)を適用」とされていても、幾何公差が数箇所加わるだけで加工の難易度が上がるからです。他にも、社内の設備だけで要求通りの精度が出せないかもしれないだとか、要求度合いによっては加工工数が増えてコストアップにつながるかもしれないといった不安などもあります。
ただ、精密さを求める部品であればあるほど、寸法公差だけに頼った品質管理には限界があります。そのため、幾何公差をうまく設計に取り入れることが重要となります。幾何公差を活用することで、部品加工に必要な項目がより明確になり、厳しい寸法公差が削減されることで作業工数が減り、結果的にコストダウンにつながる可能性も十分にあり得ます。
そう考えると、幾何公差は、やや誤解されているようでかわいそうだと思います。設計者も加工者も、皆で幾何公差への考え方や使い方を見直せば、生産性向上につながるような気がします。
ちなみに、メーカーにおける公差設計の現状については、「なかなかうまくいかぬ、公差設計推進の理想と現実」が参考になります。課題はまだまだあるようですね。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査

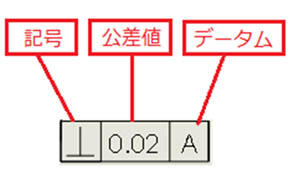 図3 幾何公差の表し方
図3 幾何公差の表し方





