「形体をコントロールする方法を覚えよう」の巻:ママさん設計者がやさしく教える「図面の読み描き超入門」(3)(2/5 ページ)
幾何公差とは?
幾何公差の「幾何」とは、「幾何学」の幾何のことだとお考えください。つまり、幾何公差とは空間におけるモノの形状や位置関係といった、“寸法以外の性質”について定めた許容範囲の値を意味します。
要するに、“寸法”をコントロールする目安が寸法公差であり、“形体”をコントロールする目安が幾何公差というわけです。
しかし、急に「形体をコントロールする」といわれても、どういうことなのかピンときませんよね。ということで、考え方の基本を手描き図面で簡単に説明します。
以下の2つの図は、道路のようにA点とB点を結ぶ水平線を描き、寸法公差(図1)と幾何公差(図2)を入れた手描きの図面です。
このうち、図1に記載されている寸法公差は、A-B間の“距離精度”を要求するもので、「距離が±0.05に入っていれば、路面のうねりはさほど気にしないよ」と解釈できます。
これに対して図2に記載されている幾何公差は、A-B間の道路の“路面精度”を要求するもので、「うねりの高低差を0.1以内に抑えた平らな路面にしてくれ」と解釈できます。これが「平面度」と呼ばれる幾何公差になり、小さな平行四辺形の記号と公差値で表現する決まりとなっています。これならば文字を連ねるよりもスッキリとして分かりやすいですよね。しかも、幾何公差の記述は“世界共通言語”なので、日本語の読めない加工者にも指示を正しく伝えることができます。
A-B間の路面の出来栄えが曖昧でいいなら寸法公差のみ適用すればいいですし、曖昧さを排除して路面の精度を上げたいなら幾何公差を適用すればよいのです。もしも距離精度と平面度の両方の要求を満たしたい場合は、2つとも図面に記述します。
単独形体と関連形体
幾何公差は、「単独形体」と「関連形体」の2つに分類されます。
単独形体とは、前述の平面度の例のように“形体そのものに対して指定できるもの”で、関連形体とは“形体と相手との関係性を指定するもの”です。
では、ここでいう“相手”とは何を指すのでしょうか?
例えば、「ソリを1mm以内にしてほしい」といわれたとき、何かしらの“測量基準”がなければソリの度合いを認識することはできませんよね。つまり、ここでいう相手とは測量基準のことであり、ソリのような形体の「姿勢」や「位置」などをコントロールするのに必要な平面や直線などがそれに当たります。こうした測量基準のことを「データム」と呼びます。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
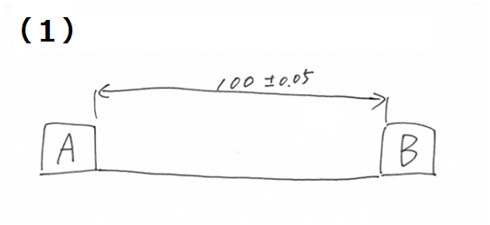 図1 「寸法公差」の入った図面
図1 「寸法公差」の入った図面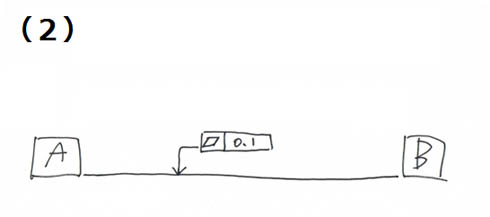 図2 「幾何公差」の入った図面
図2 「幾何公差」の入った図面





