回転する部品に指定する「振れ公差」:製図を極める! 幾何公差徹底攻略(9)(2/2 ページ)
次に、振れ公差は回転する動的な部品に指示をします。平行に並べたローラーの回転する表面の隙間を管理して部品を搬送する構造物(図6)を例に説明していきます。
軸の両端をそれぞれケースに配置した2個の軸受で保持する場合、この2つの軸受の共通軸線が製品の基準であるデータム軸になり、ローラー表面が機能面となり振れが要求されます。
幾何公差を使って図6のローラー軸を表す場合、共通軸線として表現するため一方をデータムA、もう一方をデータムBとします。
その他の幾何特性に使用しないのであれば、どちらがデータムAでもデータムBでも構いません。データムAとデータムBの共通軸線を参照していることを表すために「A-B」として表現します。
ここまでで、同軸度は静止して使用する部位、全振れ(円周振れも同様)は回転して使用する部位と使い分ければよいことを知りました。
以降では、振れ公差である円周振れと全振れの代表的な図面指示例を確認していきます。
円周振れ
JISによると、「円周振れ(Circular run-out)とは、データム軸直線を軸とする円筒面を持つべき対象物、またはデータム軸直線に対して垂直な円形平面であるべき対象物をデータム軸直線の周りに回転したとき、その表面が指定した位置または任意の位置で指定した方向に変位する大きさをいう」と定義されます。
円周振れは、任意の位置での振れのみを評価するものです。つまり、振れた領域はある一方向から見ると、まるで2次元のような領域であることが特徴です。
図8に示す図面例は、段付き軸の左右の小径側の中心軸を共通データムとして回転させたとき、大径側の任意の位置の円筒表面がデータム軸と同軸となる幅0.05mmの2円間にあれば合格品と判断されるものです。それぞれの直径に寸法公差が記入されていますが、独立の原則に従うため寸法公差とは無関係に円周振れを満足させればよいということです。
図9に示す図面例は、段付き軸の小径側の中心軸をデータムとして回転させたとき、大径側の任意の位置の円筒端面がデータム軸と直角な幅0.05mmの2面間にあれば合格品と判断されるものです。それぞれの直径や長さに寸法公差が記入されていますが、独立の原則に従うため寸法公差とは無関係に円周振れを満足させればよいということです。
全振れ
JISでは、「全振れ(Total run-out)とは、データム軸直線を軸とする円筒面を持つべき対象物またはデータム軸直線に対して垂直な円形平面であるべき対象物をデータム軸直線の周りに回転したとき、その表面が指定した方向に変位する大きさをいう」と定義されます。
全振れは、指示した面全体の振れを評価するものです。つまり、振れた領域は3次元領域であることが特徴です。
図10に示す図面例は、段付き軸の左右の小径側の中心軸を共通データムとして回転させたとき、大径側の円筒表面全体がデータム軸と同軸となる幅0.05mmの2円筒間にあれば合格品と判断されるものです。それぞれの直径に寸法公差が記入されていますが、独立の原則に従うため寸法公差とは無関係に全振れを満足させればよいということです。
図11に示す図面例は、段付き軸の小径側の中心軸をデータムとして回転させたとき、大径側の円筒端面全体がデータム軸と直角な幅0.05mmの2面間にあれば合格品と判断されるものです。それぞれの直径や長さに寸法公差が記入されていますが、独立の原則に従うため寸法公差とは無関係に全振れを満足させればよいということです。
以上、2種類の振れ公差を確認しました。回転方向の円筒外表面や回転と直角な円筒端面方向のどちらにも使えることが分かりました。
これにて、4つのグループに分類される幾何特性の全てを確認しました。次回はいよいよ最終回。幾何公差の相互関係について説明をします。(次回に続く)
◎併せて読みたい「CAD」関連ホワイトペーパー:
» 主要7製品を完全網羅! 製品選定・比較に役立つ「商用3D CADカタログ 完全版」
» 【導入事例】食品加工機械メーカー不二精機による“3D CAD推進”
関連記事
 最近のJISだと「寸法公差」ではなく「サイズ公差」なのはなぜか
最近のJISだと「寸法公差」ではなく「サイズ公差」なのはなぜか
機械メーカーで3D CAD運用や公差設計/解析を推進する筆者から見た製造業やメカ設計の現場とは。今回はJIS製図における「サイズ」「サイズ公差」「幾何公差」について考える。 「設計から製図までチャレンジしてみよう」の巻
「設計から製図までチャレンジしてみよう」の巻
図面にも触れたことのないような初心者を対象とした、図面の読み方・描き方講座。お題をクリアしながら、解説を読み進めていくことで、いつしか図面の読み描きができるようになる! 今回は、集大成として設計から製図までの一連の作業に挑戦する。 2Dと3Dの融合と、公差設計の重要性
2Dと3Dの融合と、公差設計の重要性
機械メーカーで3D CAD運用や公差設計/解析を推進する筆者から見た製造業やメカ設計の現場とは。今回は構想設計から詳細設計までのプロセスを振り返りながら、公差設計の重要性について考える。 設計者必携! 板金設計がマスターできる絵辞書
設計者必携! 板金設計がマスターできる絵辞書
これまでの「甚さんシリーズ」の解説を少し振り返った後、この連載で使うツール「板金設計の50%がマスターできる絵辞書」を紹介する。 いまさら聞けない!? 製図の素朴な疑問たち
いまさら聞けない!? 製図の素朴な疑問たち
「外形線と寸法補助線は接して描かなければならないのか」「φは『パイ』と読むのか」などいまさら聞けない素朴な質問ばかりを集めてみた。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 同じ機械なのに1号機はOK、2号機はNG 設計者を悩ませる“再現しない不具合”
- 義手とロボットの手を共通化するPSYONICのバイオニックハンド「Ability Hand」
- NVIDIAとダッソーがCEO対談 産業AI基盤構築で戦略的パートナーシップ締結
- 高精度3Dスキャナー3機種を発売、自動検査や医療分野を支援
- 設計者を支える3つのAI仮想コンパニオン 探索×科学×実現で製品開発を伴走
- 約3.5kgの力で打ち抜ける手動式卓上パンチプレス
- 強度設計の出発点 “計算”より先に考えるべきこととは?
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 令和版の健康サンダル? 否、感覚を増幅する「Nike Mind」が気になる件
- 幾何公差の基準「データム」を理解しよう
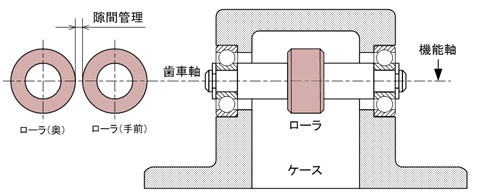 図6 両端指示の回転軸の組立状態
図6 両端指示の回転軸の組立状態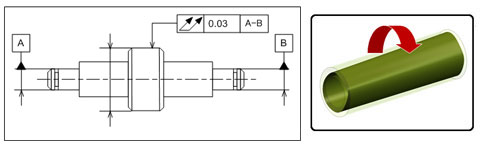 図7 振れ公差を使って指示した場合:右側の領域を示すイラストは、データム軸線を中心として回転し、対象部の表面が円筒方向に振れる領域を意味します
図7 振れ公差を使って指示した場合:右側の領域を示すイラストは、データム軸線を中心として回転し、対象部の表面が円筒方向に振れる領域を意味します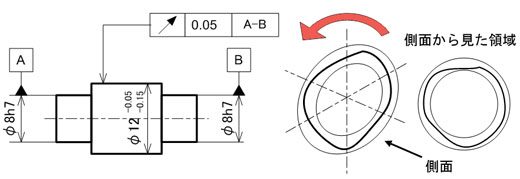 図8 円周振れの指示例と領域(円筒方向の場合):右側の領域を示すイラストは、データム軸線を中心に回転したとき、データムに同軸な2円間の領域を意味します
図8 円周振れの指示例と領域(円筒方向の場合):右側の領域を示すイラストは、データム軸線を中心に回転したとき、データムに同軸な2円間の領域を意味します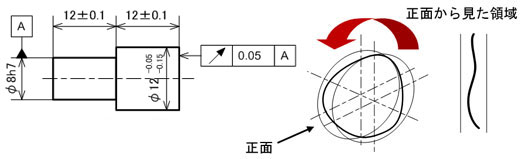 図9 円周振れの指示例と領域(円筒面に直角な端面の場合):右側の領域を示すイラストは、データム軸線を中心に回転したとき、データムに直角な任意の位置における2面間領域を意味します
図9 円周振れの指示例と領域(円筒面に直角な端面の場合):右側の領域を示すイラストは、データム軸線を中心に回転したとき、データムに直角な任意の位置における2面間領域を意味します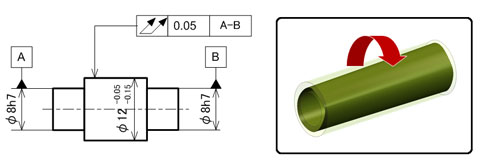 図10 全振れの指示例と領域(円筒方向の場合):右側の領域を示すイラストは、データム軸線を中心に回転したとき、データムに同軸な2円筒間の領域を意味します
図10 全振れの指示例と領域(円筒方向の場合):右側の領域を示すイラストは、データム軸線を中心に回転したとき、データムに同軸な2円筒間の領域を意味します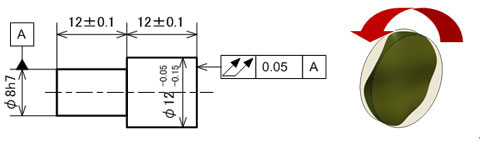 図11 全振れの指示例と領域(円筒面に直角な端面の場合):右側の領域を示すイラストは、データム軸線を中心に回転したとき、データムに直角な端面全体の2面間領域を意味します
図11 全振れの指示例と領域(円筒面に直角な端面の場合):右側の領域を示すイラストは、データム軸線を中心に回転したとき、データムに直角な端面全体の2面間領域を意味します






