硬さを表すヤング率は“材料のバネ定数”:仕事にちゃんと役立つ材料力学(7)(3/3 ページ)
力の状態とタテとヨコとが織りなす弾性係数
さて、ヤング率については、シッカリとイメージできましたか? ヤング率は別名、「縦弾性係数」であるということは説明しました。僕は初めてこの言葉を聞いたとき、「縦弾性係数があるなら、横弾性係数はあるのか?」と思いました。ここではそれについて解説したいと思います。
実はこれまで何度も登場した応力-ひずみ線図であいまいにしてきたことがあります。これはどんな実験により得られたグラフなのか? ということです。
部品には、さまざまな大きさの力がさまざまな方向から掛かるわけですが、いくつかの種類に分類することができます。「こんな力」「あんな力」といっても、力の状態を伝えるのには限度があるようで、大体5つに集約して力の状態をできるだけ正確に伝えます(図7)。
この5つの状態は、消しゴムで表現できますから、手元に消しゴムがある人はこの5つの状態を再現してみてください。同じ長さ分なら、引っ張るよりも圧縮する方が力が必要だったりします。消しゴムが外からの力に抵抗しているのが感触を通して伝わってきます(写真1)。
応力―ひずみ曲線はどんな実験により得られたグラフなのか。ヤング率つまり縦弾性係数の測定実験は、引張り力を掛けた状態で行います。古典的な方法から近代的な方法までさまざまな測定方法があります。これまで登場してきた応力―ひずみ曲線はその測定方法に従ってデータが採取されグラフが描かれているわけです。
ここで測定方法を詳しく説明すると横道にそれるので、Webサイトの紹介で切り抜けたいと思います。
このサイトではヤング率について、アニメーションなどを使いながら分かりやすく説明しています。ヤング率のまとめと整理という意味でも参考にしてみてください。このサイトの中にヤング率の測定方法の説明もあります。
引張りの力の場では、垂直応力がメインとなります。つまり縦弾性係数は、垂直応力と垂直ひずみの間に成り立つ、比例定数ということになります。
ここで最初の「横弾性係数はあるのか?」という疑問に戻りますが、その答えは「Yes」です。これはせん断応力とせん断ひずみの間に成り立つ、比例定数です。記号では「G」で表されます。せん断ひずみ、せん断応力については、これまでの回を読んで復習してみてください。
縦弾性係数と横弾性係数について、まとめておきます。1つ目の式は、ぜひ覚えておいてください。今回はギリシア文字で覚えておくといいでしょう。「シグマ、イコール、イー、イプシロン」と呪文のようにリズムで覚えてください(図8)。
ヤング率に弟がいた。その名はポアソン比
鋼材でできた円柱を想像してください。別に鋼材でなくても、ソーセージでも構いません。その円柱を両方から引っ張ると、円柱は伸びます。その円柱の直径はどうなるでしょう? 引っ張った方向とは直角に縮みます。直径が小さくなるので、円柱の断面積も小さくなるわけです。
さっき写真で登場した消しゴムを引っ張ってみました。引っ張った方向に伸びるのと、引っ張った方向と直角方向に縮みます。
伸びているのはハッキリと分かりますが、縮んでいるのが分かるでしょうか。でも引っ張れば、その方向とは直角に縮むのは直感的に理解できるでしょう。
引っ張った方向のひずみを「縦ひずみ」、引っ張った方向とは直角方向のひずみを「横ひずみ」といいます。「ひずみ」とは、元々力を受けたときの変形量を元の長さで割ったものです。それに、縦と横という方向の概念が加わったのが、縦ひずみと横ひずみと思ってください。そしてさらにこの縦ひずみと横ひずみの比を「ポアソン比」といいます(図9)。
ポアソン比もヤング率と同じように、材料固有のものです。そしてヤング率と同じくらい大切な定数です。ヤング率の弟分くらいに思っていてください。
◇
今回は盛りだくさんの内容でした。ポアソン比をもう少し突っ込んで解説したいのですが、それは次回ということでご勘弁ください。
とにかく、ヤング率とポアソン比は材料固有の値で、その材料の強さを表す重要な定数であるということをアタマの中に入れておいてくださいね。(次回に続く)
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現
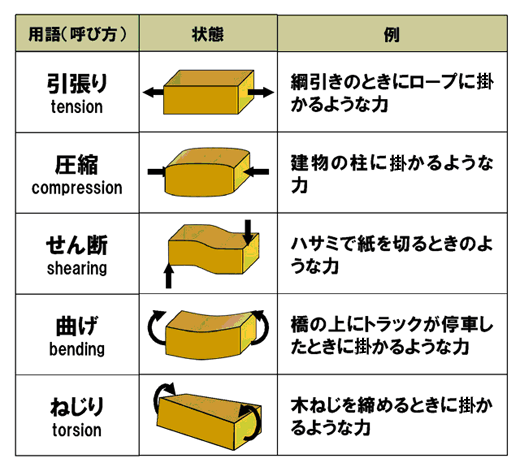 図7 用語とその状態
図7 用語とその状態  写真1 消しゴムで試してみよう
写真1 消しゴムで試してみよう 
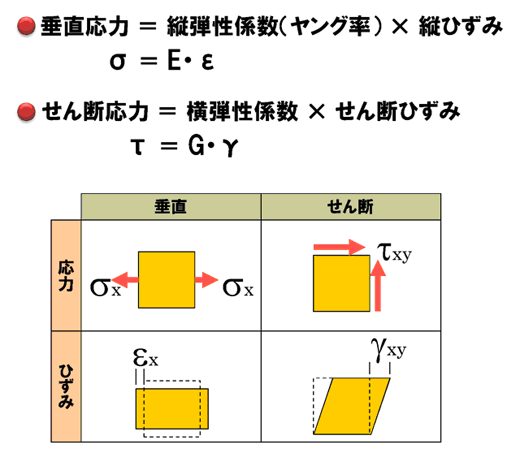 図8 縦弾性係数と横弾性係数のまとめ――「シグマ、イコール、イー、イプシロン……」
図8 縦弾性係数と横弾性係数のまとめ――「シグマ、イコール、イー、イプシロン……」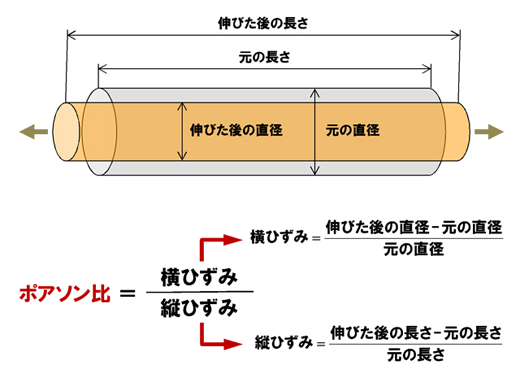 図9 ポアソン比とは
図9 ポアソン比とは






