硬さを表すヤング率は“材料のバネ定数”:仕事にちゃんと役立つ材料力学(7)(2/3 ページ)
金属の「硬さ」を示す定数「ヤング率」
これまでの応力―ひずみ曲線の中のオレンジ色で示してきた領域、つまり、ひずみと応力が比例する領域だけをクローズアップして考えてみましょう。ここで、第5回にて解説したフックの法則(*1)を思い出してください。
図3グラフの横軸の「伸びた長さ」は、非常に乱暴ではありますが、「ひずみ」と定性的に同じものです。また、このグラフの縦軸の「応力」も、これまた乱暴ではありますが、「応力」と定性的に同じです。そう考えると、応力―ひずみ曲線の比例部分と、フックの法則は同じようなものであるということが分かります。
フックの法則のバネ定数に当たるものを、応力―ひずみ曲線では「ヤング率」といいます。誤解を恐れずいい切れば、ヤング率は「材料のバネ定数」ということになります。バネにも、軟らかいバネと硬いバネがあるように、材料にも、軟らかい材料と硬い材料があります。その程度を表すのがヤング率です。材料の定数の中で、一番、重要な定数ですので忘れないでおいてください。ヤング率は、英語で「Young's modulus」、別名「縦弾性係数」といいます。また記号では「E」と書きます。もちろん材料によってヤング率は異なります。
そういうわけで、第5回で出した課題の解答は、以下のようになります(図4)。
図4の式を変形してみます。両辺を「ひずみ」で割ると、以下図5のようになります。
ヤング率の単位を確認しておきましょう。図5の式を見れば明らかですね。ひずみには単位がないので、ヤング率の単位は応力の単位そのものになります。[Pa](パスカル)ですね。金属材料のヤング率は一般的に大きな値なので、[MPa](メガ・パスカル)や[GPa](ギガ・パスカル)で表されます。
さて、もう一歩だけ踏み込んで、このグラフを分析してみましょう。応力―ひずみ曲線の比例領域だけに注目しましょう。まず、応力とひずみは比例するので、グラフは直線になります。
図6には2つの材料の応力―ひずみ曲線の比例部分が描かれています。同じひずみでも、材料Aの方が材料Bより応力が大きくなります。また、同じ応力でも材料Bの方が材料Aよりひずみが大きくなります。
フックの法則に立ち戻り、上記の“応力”を“力”、“ひずみ”を“伸びた長さ”と置き換えて考えてみましょう。
図6右のグラフを見てください。例えば、同じ力でも材料Bの方が材料Aより伸びた長さが長い、ということになります。
「材料Aと材料Bのバネ、どちらが軟らかいでしょうか?
そしてどちらが硬いのでしょう?」
答えはカンタンです。材料Aのバネが硬いバネ、材料Bが軟らかいバネです。これは材料そのものにもいえることなのです。
。oO 筆者のつぶやき
物理の天才・ヤングの生い立ち
ヤング率の「ヤング」は人の名前です。フックのときと同じように、人物探訪してみましょう。ヤング率がより身近なものになることを期待しつつ。ヤングのフルネームは、トーマス・ヤングです。フックの没後、70年を経てからイギリスで生まれました。メインは物理学です。神童を地でいく天才肌だったらしく、2歳で字を読み、4歳で聖書を2回も読んだらしいです。そしてさらに14歳のときには、ラテン語で自伝を書いたとか……。
学生時代は、天才、奇才と呼ばれ、卒業後には特に光の分野で大活躍したようです。さらに、医学、生物学から、果ては諸外国語までも使いこなし、エジプトの象形文字の研究までやったツワモノだそうです。
肩書きはさらにすごくて、物理学者のほかにも、医師、度量衡委員、自然哲学教授、海軍省顧問、古典学者、考古学者、保険会社監事など、さまざまな才能を発揮したようです。そして、さらにヤング率。この世に材料力学のある限り、この名前は永久に不滅です。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現
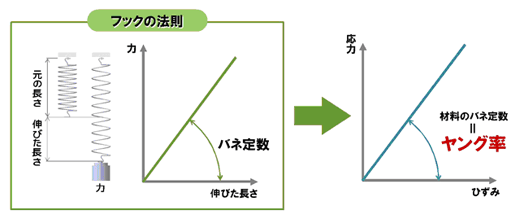 図3 フックの法則
図3 フックの法則 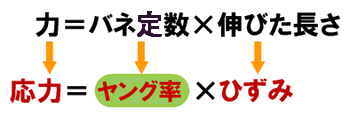 図4 第5回で出した問題の解答
図4 第5回で出した問題の解答 図5 ヤング率を求める公式
図5 ヤング率を求める公式 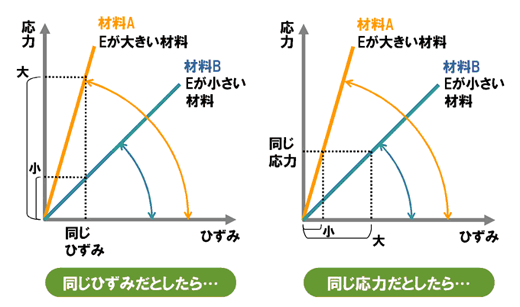 図6 ヤング率を求める公式
図6 ヤング率を求める公式 





