少し冒険して、円管層流のヌセルト数を求めてみよう!:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(16)(1/5 ページ)
CAE解析とExcelを使いながら冷却系の設計を“自分でやってみる/できるようになる”ことを目指す連載。連載第16回は、少し冒険して、円管層流のヌセルト数を求めてみましょう。果たして、うまくいくでしょうか?
今回は少し冒険してみます。円管層流のヌセルト数を求めてみましょう。できるでしょうか? あと、おまけも付けておきます。
円管層流のヌセルト数:解析モデル
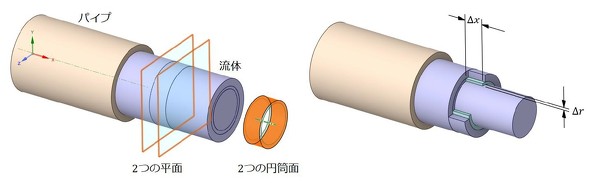
図1に、円形パイプ内を流れる流体を示します。
図1左図のように、流体を2つの平面と2つの円筒面で分割します。すると、図1右図のように、厚さΔr、長さΔxの微小な円筒が出来上がります。この微小な円筒に注目します。
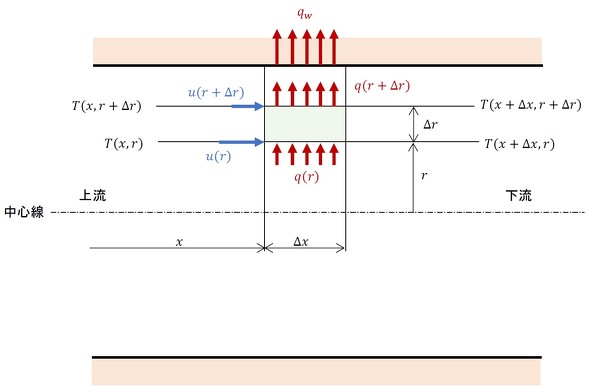
図2に、微小円筒の断面を示します。
半径rの位置の熱流束をq(r)、半径r+Δrの熱流束をq(r+Δr)とします。軸方向の位置xにおける温度をT(x,r)、T(x,r+Δr)、軸方向の位置x+Δxにおける温度をT(x+Δx,r)、T(x+Δx,r+Δr)とします。流速についても、軸方向の位置xにおける流速をu(x,r)、u(x,r+Δr)、軸方向の位置x+Δxにおける流速をu(x+Δx,r)、u(x+Δx,r+Δr)とします。
熱収束の方向と半径方向を合わせるため、熱流束を上向きとしています。これは、流体から管に熱が移動することを意味します。逆に、管から流体に熱が移動する場合は、熱流束はマイナス値となります。
円管層流のヌセルト数:微分方程式の導出
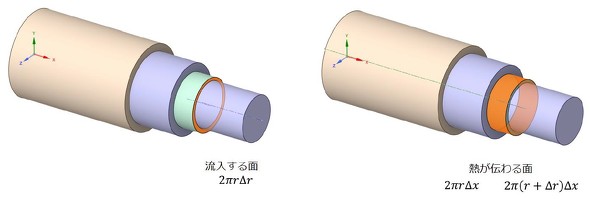
図3に、流入する面と熱が伝わる面の面積を示します。
流速×面積=流量、熱流束×面積=熱の移動量となるので、微小円筒に流入する熱は式1で表されます。
ここでいう「熱」という表現は正確ではなく、この式の第1項は「比熱×流量×密度×温度」を求めています。これは、0[degC]から温度T[degC]まで上昇させるのに必要な熱量、すなわち0[degC]を基準とした流体の持つ熱量です。体積変化のないエンタルピーのようなものと解釈できるため、便宜上「エンタルピー」と呼ぶことにします。
出ていくエンタルピーは式2となります。
以下は、平均流速を求めているのですが、変化分との引き算ではなく足し算なので、いずれ微小項の削除のところで変化分はなくなります。よって、次のように表します。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン社員が技能五輪国際大会の工業デザイン技術職種で日本代表に
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本

 式1
式1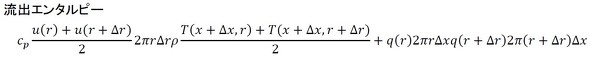
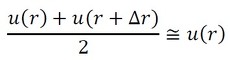 式3
式3





